Sidney J Faria-e-Sousa1; Gustavo Victor2
DOI: 10.17545/eoftalmo/2018.0011
RESUMO
O diagrama em cruz é um artifício gráfico projetado para facilitar a anotação dos resultados da retinoscopia e auxiliar na transposição de lentes. Existem duas maneiras de construir esse diagrama. Um deles é muito mais amigável que o outro.
Palavras-chave: Astigmatismo; Refratometria; Erros de Refração.
ABSTRACT
Cross diagram is a graphical expedient designed to facilitate the annotation of retinoscopy results and assist in lenses transposition. This diagram can be built in two ways, one of which is much easier than the other.
Keywords: Astigmatism; Refractometry; Refractive errors.
RESUMEN
El diagrama en cruz es un artificio gráfico proyectado para facilitar la anotación de los resultados de la retinoscopía y auxiliar en la transposición de lentes. Hay dos maneras de construir ese diagrama. Una de ellas es mucho más amigable que la otra.
Palabras-clave: Astigmatismo; Refratometría; Errores de Refracción
INTRODUÇÃO
O diagrama em cruz é um artifício gráfico projetado para facilitar a anotação dos resultados da retinoscopia e da transposição de lentes. 1 O princípio que norteia a sua construção é que, seja qual for o tipo de erro refrativo, ele sempre pode ser representado pela combinação de dois cilindros ortogonais. Quando os cilindros têm sinais e poderes idênticos, formam uma lente esférica; quando têm sinais e poderes diferentes, configuram uma lente tórica; quando um deles tem valor zero, a combinação representa uma lente cilíndrica simples.
Classicamente, um diagrama em cruz consiste em uma linha vertical e uma horizontal, cruzadas ao meio. Nesse esquema, inserimos as inclinações e os poderes dos meridianos mais curvos do par de cilindros ortogonais que caracteriza a correção da ametropia (Figura 1). O uso dos meridianos mais curvos possivelmente decorre do fato de eles serem os únicos que contêm o poder creditado ao cilindro. Entretanto, o maior problema de trabalharmos com esses meridianos é que o diagrama não fornece as posições dos eixos dos cilindros, informação crítica para a transcrição das prescrições ópticas. Para acessarmos essas informações, frequentemente precisamos realizar cálculos desconfortáveis. O objetivo deste trabalho é mostrar que existe alternativa mais amigável para a construção de um diagrama em cruz, desprovido desse problema.
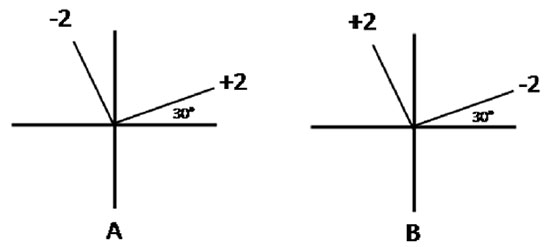
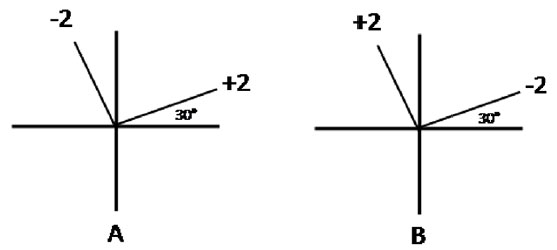
DIAGRAMA EM CRUZ CLÁSSICO
O diagrama A da Figura 1 é um exemplo do que os cursos de refratometria classicamente ensinam. Ele expressa a potência e a inclinação dos meridianos mais íngremes dos cilindros ortogonais que corrigem o erro de refração. No desenho, os cilindros de + 2 D apresentam o meridiano mais curvo a 30º enquanto que o cilindro de 2 D apresenta o mesmo meridiano a 120º. Esse diagrama se baseia, portanto, na posição dos meridianos mais curvos dos cilindros corretores da ametropia. 1
O problema com este diagrama é que ele não mostra a direção dos eixos dos cilindros (Figura 1A); informação crítica para transcrevê-lo em prescrição óptica. Esse inconveniente é consequência direta da violação do princípio de que o eixo é o que caracteriza a direção do cilindro. 2 Como os eixos são sempre perpendiculares aos meridianos mais curvos, para encontrá-los é necessário mudarmos de 90º as direções mostradas no diagrama A. Adicionando 90º à inclinação do cilindro de + 2 D, obtemos a direção do seu eixo, que é de 120º. Subtraindo 90º da direção do cilindro de 2 D obtemos a inclinação do seu eixo, que é de 30º. A transcrição desse diagrama em uma combinação de cilindros passa a ser + 2 cil 120º x 2 cil 30º. Embora esses cálculos sejam simples, eles podem se tornar mentalmente desgastantes particularmente quando o par de cilindros corretores faz ângulo com o diagrama, como no exemplo acima.
DIAGRAMA EM CRUZ BASEADO NOS EIXOS DOS CILINDROS CORRETORES
O diagrama B da Figura 1 mostra os mesmos cilindros do diagrama A, mas expressos por seus eixos, e não pelos seus meridianos de curvatura máxima. A linha inclinada da esquerda corresponde a um cilindro de + 2 D com o eixo a 120 º e a linha da direita, a um cilindro de 2 D com o eixo a 30º. Vale ressaltar que os meridianos mais curvos (não mostrados no desenho) permanecem em suas posições originais. É precisamente esse fato que valida as operações algébricas de um diagrama em cruz baseado nos eixos dos cilindros. Além disso, o diagrama B reproduz a posição das linhas focais do erro de refração devido ao alinhamento obrigatório dos cilindros corretivos com as linhas focais do intervalo de Sturm que define a ametropia. Enquanto que o sinal positivo indica que a linha focal está além da retina, o negativo implica que a linha focal está dentro do olho. Operando com os eixos dos cilindros, este diagrama pode ser diretamente convertido em prescrições ópticas, sem a necessidade de transposições angulares.
INTERPRETAÇÃO DO DIAGRAMA EM CRUZ BASEADO NOS EIXOS DOS CILINDROS CORRETORES
O diagrama em cruz baseado nos eixos dos cilindros retrata as potências e os eixos dos cilindros que neutralizam o erro de refração (Figura 2). Dois cilindros ortogonais da mesma potência e sinal constituem uma lente esférica (Figuras 2B e 2D). Dois cilindros ortogonais com potência e sinal diferentes representam uma lente esferocilíndrica (tórica) (Figura 2A). Dois cilindros ortogonais em que um deles tem valor zero correspondem a uma lente cilíndrica simples (Figuras 2C e 2E).
O diagrama A no centro da Figura 2 representa uma lente que admite três interpretações: uma combinação de dois cilindros, uma combinação de uma esfera positiva com um cilindro negativo e uma combinação de uma esfera negativa com um cilindro positivo. A verificação que o diagrama A é uma combinação de dois cilindros é evidente. Basta lê-lo literalmente, ou seja, + 2 cyl 120º x - 2 cyl 30º. A combinação de uma esfera positiva com um cilindro negativo pode ser visualizada como a associação de uma esfera + 2 D com um cilindro de - 4 × 30º, identificados como B e C respectivamente, na parte superior da Figura 2. Adicionando algebricamente o poder óptico dos braços correspondentes de B e C obtemos a lente A que é transcrita como + 2 x – 4 cil 30º. A combinação de uma esfera negativa com um cilindro positivo pode ser imaginada como a associação de uma esfera de - 2 D com um cilindro de + 4 × cil 30º, identificados como D e E, respectivamente, na parte inferior da Figura 2. Adicionando algebricamente o poder óptico dos braços correspondentes de D e E obtemos a lente A que é transcrita como – 2 x + 4 cil 120º.
Para construir um diagrama em cruz a partir da lente corretora de um erro de refração, devemos proceder da seguinte forma: (1) Desenhe três diagramas em cruz, cada qual com o par de linhas que conterão os eixos dos cilindros ortogonais que representam a ametropia, como em A, B e C (ou A, D e E) da Figura 2. Lembre-se de que qualquer lente pode ser representada por um par de cilindros ortogonais. (2) Converta o primeiro diagrama em uma lente esférica, rotulando ambas as linhas com o valor nominal do componente esférico do erro de refração, como em B e D. (3) Converta o segundo diagrama em uma lente cilíndrica, rotulando a linha apropriada com o poder e o eixo do cilindro que corrige o astigmatismo, assegurando que a linha parceira seja identificada com o número zero, como em C e E. (4) Adicione algebricamente o poder óptico dos braços correspondentes desses dois diagramas e transfira o resultado para o diagrama vazio, o qual ira exibir graficamente a correção da ametropia, como em A.
Como um único diagrama em cruz, como A da Figura 2, representa diferentes combinações de esferas e cilindros, ele torna-se ferramenta útil para transpor prescrições de erros de refração em combinações de cilindros ou de esferas com cilindros.
RETINOSCOPIA E O DIAGRAMA BASEADO NOS EIXOS DOS CILINDROS
Na retinoscopia, o examinador compara o movimento de uma faixa de luz projetada na superfície do olho com o reflexo luminoso retiniano. O último é a imagem formada pela luz refletida da retina. 3 Quando a córnea é tórica, os reflexos luminosos retinianos, correspondentes aos meridianos principais da mesma, coincidem com as linhas focais do intervalo de Sturm e, por extensão, com os cilindros que corrigem a ametropia. 4 Assim, se um dos reflexos luminosos retinianos estiver inclinado de 120º e a potência necessária para neutralizá-lo for um cilindro de + 2 D, será necessário uma correção de + 2 cil 120º para conjugar a linha focal correspondente ao orifício de observação do retinoscópio. No diagrama em cruz, marcamos o poder desse cilindro na direção de 120º (Figura 3). Se o outro reflexo luminoso retiniano requer um cilindro de 2 D para neutralizá-lo, uma correção de - 2 cil 30 º será necessária para conjugar a linha focal correspondente ao orifício de observação do instrumento.No diagrama em cruz, registramos o poder desse cilindro na direção de 30º (Figura 3). É importante enfatizar que este tipo de anotação difere da clássica de 90º.

REFERÊNCIAS
1. Rubin M. Optics for Clinicians. 2nd ed. Gainesville, FL: TRIAD Scientific Publisher, 1977, p.85.
2. Faria-e-Sousa SJ, Alves MR. Astigmatism: Aberration or ametropia? eOftalmo. 2018; 4 (1): 26-32. http://dx.doi.org/10.17545/eoftalmo/2018.0004
3. Corboy JM. The Manual Book - a manual for beginners. 2nd ed. Thorofare, NJ: Charles B Slack Inc, 1982.
4. Faria-e-Sousa SJ. Retinoscopia. In: Refratometria ocular e a Arte da Prescrição Médica. Alves MR ed. 3 ed. Rio de Janeiro, RJ: Cultura Médica, 2013. p. 5-15.

Financiamento: Declaram não haver
Parecer CEP: Não aplicável
Conflito de interesses: Declaram não haver
Recebido em:
21 de Maio de 2018.
Aceito em:
11 de Junho de 2018.