RESUMO

OBJETIVO: Apesar de a análise vetorial ser amplamente utilizada na literatura, tanto para a descrição de características, como na análise de mudanças no astigmatismo, poucos são os artigos que apresentam a racionalidade do método. Em nossa revisão, apresentamos os pontos mais importantes dos métodos propostos por Alpins e por Thibos.
MÉTODOS: O Pubmed foi pesquisado, em 29 de junho de 2016, para artigos em inglês, com resumo, empregando-se os termos (astigmatism) AND (vector analysis) AND (Alpins) OR (Thibos), independentemente da data ou tipo de publicação.
RESULTADOS: Treze artigos, de 228 referências, foram incluídos em nossa revisão. Conclusões: O método proposto por Thibos é o mais apropriado para descrições objetivas do astigmatismo. O método de Alpins, por outro lado, é o mais indicado para análises referentes a mudanças no astigmatismo.

Palavras-chave: Astigmatismo. Erro refrativo. Córnea.

ABSTRACT

AIM: Although much has been published on vector-based analysis of astigmatism, the reason why vectors precisely describe astigmatism features, or even changes in its characteristics, has been discussed only on a few articles. Our review intends to highlight the essential features of both methods proposed by Alpins and Thibos.
METHODS: Pubmed was searched for papers in English, containing abstracts, on June 29th 2016 for (astigmatism) AND (vector analysis) AND (Alpins) OR (Thibos), regardless of the date of publication or the study design.
RESULTS: Thirteen papers, out of 228 references, were included in our review. Conclusions: The method proposed by Thibos is suitable whenever an objective description of astigmatism is aimed. However, the method proposed by Alpins may provide detailed information on the assessment of changes in astigmatism.

Keywords: Astigmatism; Refractive error; Cornea;

INTRODUÇÃO

“Vetor” é um termo matemático definido pela magnitude e direção. O astigmatismo, definido por uma força cilíndrica e um eixo (refrativo), ou por uma magnitude e um meridiano (corneano), encaixa-se nesta descrição.⁽¹⁾ Tanto o astigmatismo quanto os vetores astigmáticos empregam as mesmas unidades de medida: dioptrias e graus; porém, o astigmatismo é uma entidade mensurável, enquanto vetores só podem ser calculados ⁽²⁾ Uma análise precisa e completa do astigmatismo deve levar em conta o seu caráter vetorial ⁽³⁾ por isto, a análise baseada em vetores tem sido amplamente utilizada na literatura. ^(2,4,5)

O objetivo do presente estudo foi fazer uma revisão sistemática da literatura sobre a justificativa da análise vetorial do astigmatismo. A abordagem proposta por Alpins e a descrita por Thibos e seus colaboradores foram incluídas em nosso estudo.

MÉTODOS

Esta revisão sistemática foi estruturada de acordo com as recomendações dos Preferred Reporting Items for Systematic Review and Meta-analysis Protocols (PRISMA-P), de 2015.⁵ O PubMed/MEDLINE foi pesquisado em 29 de junho de 2016 para (astigmatismo) E (análise vetorial) E (Alpins OU Thibos): independentemente da data de publicação ou projeto do estudo. Os limites impostos foram considerar apenas documentos escritos em inglês contendo resumos. Esta pesquisa inicial obteve 228 referências. Dois revisores (GF, RA) rastrearam de forma independente entre si os registros obtidos a partir da busca eletrônica e excluiram os estudos obviamente irrelevantes. Divergências de opiniões foram resolvidas por meio de discussão com um terceiro autor (MA). Nenhum dos revisores tinha conhecimento dos títulos dos periódicos, dos autores do estudo ou das instituições. O fluxograma é mostrado na Figura 1.

Figure 1. Fluxograma.

RESULTADOS

Foram incluídos 13 artigos em nossa revisão. ^{(1, 2, 3, 4)} Tais artigos forneceram informações sobre os motivos da análise vetorial ^{(1, 2, 7, 8, 9, 11, 13, 14)} ou ressaltaram a sua importância clínica. ^{(3, 4, 6, 10, 12)}

DISCUSSÃO

O método proposto por Thibos e colaboradores aborda o astigmatismo ceratométrico, incluindo qualquer eventual componente esférico presente, na forma vetorial retangular, como a seguir: ^{(3, 13, 14)}

• Média da leitura ceratométrica (M);

• Meridiano do máximo poder positivo ()

• Componente do vetor ao longo do meridiano de 0º

• (J₀)=[-(_{Koblíquo-Kplano})/2] × cos 2;

• Componente do vetor ao longo do meridiano de 45º

• (J₄₅)=[-(_{Koblíquo-Kplano})/2] × sen 2;

• Vetorde poder astigmático (APV)=(J₀²+J₄₅²)^1/2;

• Vetor de blur total (Blur)=(M2+J₀²+J₄₅²)^1/2

Se, em vez disso, for representado um erro refrativo esferocilíndrico, então M será igual ao equivalente esférico e o astigmatismo ceratométrico será substituído pelo poder refrativo do cilindro. É conveniente interpretar M, J₀ e J₄₅ geometricamente como sendo as coordenadas (x, y, z) de um ponto em um espaço dióptrico tridimensional: B é o vetor desenhado a partir da origem da coordenada desse espaço até o ponto (M, J₀, J₄₅); APV é o ponto (J₀, J₄₅) no plano astigmático. ¹⁴ A Figura 2 mostra a representação gráfica desses vetores.

Figura 2. Representação de vetores de Thibos em um espaço tridimensional (APV = vetor de poder astigmático; B = blur total; J₀ = componente do vetor junto ao meridiano de 0º; J45 = componente do vetor junto ao meridiano de 45º; M = poder médio, x = eixo da média da leitura ceratométrica ou equivalente esférico; y = eixo do meridiano de 0º; z = eixo do meridiano de 45º; 2α = meridiano de máximo poder positivo). Adaptado de: Thibos LN, Wheeler W, Horner D. Power vectors: an application of Fourier analysis to the description and statistical analysis of refractive error. Optom Vis Sci. 1997;74(6):367-75.

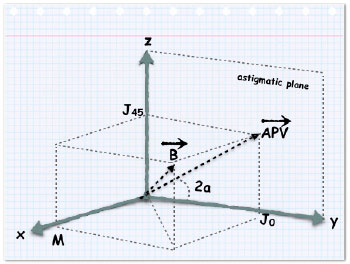
O conceito matemático de ortogonalidade de vetores simplifica os problemas práticos envolvendo combinação, comparação e análise estatística tanto das lentes esfero/cilíndricas quanto dos erros ceratorrefrativos. ¹⁴ Em outras palavras, o método proposto por Thibos e colaboradores é perfeitamente adequado para a análise descritiva de astigmatismo. ⁽³⁾

O princípio subjacente à utilização do método de Alpins baseia-se em três vetores principais, como descrito abaixo;

• O efeito almejado da cirurgia astigmática, isto é, a quantidade de tratamento necessária e sua direção. Esse efeito é chamado de vetor-alvo de astigmatismo induzido (TIA).

• O efeito cirúrgico real, que corresponde ao vetor de astigmatismo induzido cirurgicamente (SIA).

• O vetor diferença (DV), que mede a quantidade e a orientação do tratamento do astigmatismo necessárias para que seja alcançado o objetivo inicial, proporcionando assim um parâmetro cirúrgico que mede de forma eficaz o erro quanto à magnitude e ao eixo. O DV é uma medida absoluta de êxito e deve ser de preferência zero.

A Figura 3 mostra como esses vetores são graficamente calculados a partir do diagrama polar do astigmatismo até o traçado do vetor de ângulo duplo.

Figura 3. Cálculos gráficos dos vetores astigmáticos de Alpins. 3A) Diagrama polar de astigmatismo: mostrando magnitudes de astigmatismo pré-operatório, pós-operatório e alvo em suas direções reais (meridiano oblíquo da córnea ou eixo de poder do cilindro negativo - α_Pós, α_Pré e α_T respectivamente). 3B) Diagrama polar do astigmatismo de ângulo duplo: os valores do eixo do astigmatismo foram dobrados (portanto, 2α_Pós, 2α_Pré e 2α_T), mas as magnitudes dos vetores permanecem inalteradas, como é necessário para a representação do vetor. 3C) As linhas tracejadas são vetores, com as setas indicando sua direção (DV = vetor diferença; SIA = vetor induzido cirurgicamente; TIA = vetor-alvo induzido). Adaptado de: Alpins N, Goggin M. Practical Astigmatism Analysis for Refractive Outcomes in Cataract and Refractive Surgery. Surv Ophthalmol. 2004;49(1):109-22.

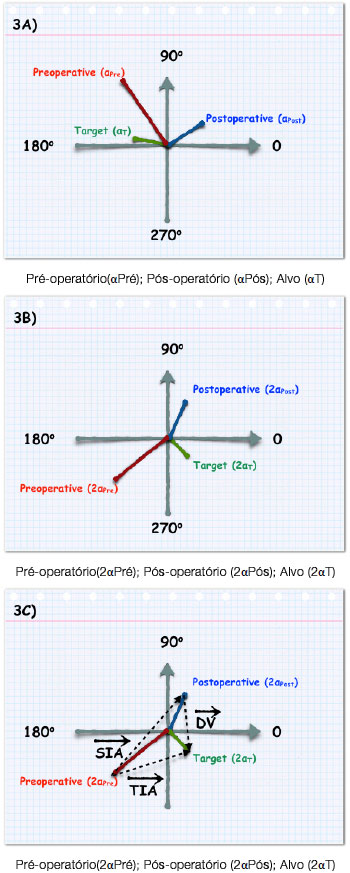
Embora o esquema gráfico do método de Alpins seja simples, os cálculos trigonométricos sequenciais necessários para estimar as magnitudes de TIA, SIA e DV podem ser problemáticos no contexto clínico, e estão fora do escopo desta revisão. Produtos comerciais de software estão disponíveis no momento para facilitar essa tarefa. ⁽¹¹⁾

As várias relações entre esses vetores fornecem parâmetros objetivos para avaliar se o tratamento está no eixo ou fora dele, se o tratamento foi demasiado ou insuficiente e se os ajustes necessários foram feitos, caso a correção de astigmatismo tenha sido repetida. ^{(1, 7, 11)} Entre esses parâmetros, alguns dos mais amplamente utilizados estão listados abaixo: ^{(1, 11)}

• Índice de Correção (IC): Calculado determinando-se a relação do SIA com o TIA (o que a cirurgia realmente induz versus o que a cirurgia pretendia induzir). Essa relação é calculada dividindo-se o SIA (efeito real) pelo TIA (efeito-alvo). O IC de preferência é 1,0 (maior do que 1,0, se houver hipercorreção e menor que 1,0, se houver hipocorreção).

• Magnitude do erro (ME): A diferença aritmética entre as magnitudes do SIA e do TIA. A magnitude do erro é positiva para hipercorreções e negativa para hipocorreções.

• Índice de Sucesso (IS): Calculado dividindo-se o DV pelo TIA (tratamento almejado). O IS é uma medida relativa de êxito e de preferência deve ser 0.

• Coeficiente de ajuste (CA): (obtido ao dividir-se o TIA pelo SIA; o inverso do IC), para ajustar a magnitude do tratamento futuro para astigmatismo (TIA). Seu valor deve ser de preferência 1,0.

Em resumo, embora ambos os métodos avaliem o astigmatismo de córnea ou de refração através de análises de vetores, o método proposto por Thibos é adequado sempre que se desejar uma descrição objetiva do astigmatismo. Se, no entanto, estiver sendo procurada qualquer alteração no astigmatismo, então o método de Alpins pode fornecer dados mais valiosos.

REFERÊNCIAS

1. Alpins N, Goggin M. Practical astigmatism analysis for refractive outcomes in cataract and refractive surgery. Surv Ophthalmol. 2004;49(1):109-22. http://dx.doi.org/10.1016/j.survophthal.2003.10.010

2. Alpins N, Stamatelatos G. Vector analysis applications to photorefractive surgery. Int Opthalmol Clin. 2003;43(3):1-27.

3. Freitas GO, Ambrósio-Jr R, Ramos I, Lopes B, Valbon BF, Botteon C, et al. Astigmatic vector analysis of posterior corneal surface: a comparison among healthy, forme fruste, and overt keratoconic corneas. Am J Ophthalmol. 2016;167(7):65-71. http://dx.doi.org/10.1016/j.ajo.2016.04.008

4. Kunert KS, Russmann C, Blum M, Sluyterman G. Vector analysis of myopic astigmatism corrected by femtosecond refractive lenticule extraction. J Cataract Refract Surg. 2013;37(5):759-69. http://dx.doi.org/10.1016/j.jcrs.2012.11.033

5. Shamseer L, Moher D, Clarke M, Ghersi D, Liberati A, Petticrew M, Shekelle P, Stewart LA, the PRISMA-P Group. Preferred reporting items for systematic review and meta-analysis protocols (PRISMA-P) 2015: elaboration and explanation. BMJ. 2015;349:g7647. https://dx.doi.org/10.1136/bmj.g7647

6. Alpins N, Ong JK, Stamatelatos G. Corneal Topographic Astigmatism (CorT) to Quantify Total Corneal Astigmatism. J Refract Surg. 2015;31(3):182-6. http://dx.doi.org/10.3928/1081597X-20150224-02

7. Alpins N. A new method of analyzing vectors for changes in astigmatism. J Cataract Refract Surg. 1993;19(7):524-33. http://dx.doi.org/10.1016/S0886-3350(13)80617-7

8. Alpins N. New method of targeting vectors to treat astigmatism. J Cataract Refract Surg. 1997;23(1):65-75. http://dx.doi.org/10.1016/S0886-3350(97)80153-8

9. Alpins N. Vector analysis of astigmatism changes by flattening, steepening, and torque. J Cataract Refract Surg. 1997;23(12). http://dx.doi.org/10.1016/S0886-3350(97)80021-1

10. Alpins N. Treatment of irregular astigmatism. J Cataract Refract Surg. 1998;24(5):634-46. http://dx.doi.org/10.1016/S0886-3350(98)80258-7

11. Alpins N. Astigmatism analysis by the Alpins method. J Cataract Refract Surg. 2001;27(1):31 -49. http://dx.doi.org/10.1016/S0886-3350(00)00798-7

12. Piñero DP, Alió JL, Tomás J, Maldonado MJ, Teus MA, Barraquer RI. Vector Analysis of Evolutive Corneal Astigmatic Changes in Keratoconus. Invest Ophthalmol Vis Sci. 2011;52(7):4054-62. http://dx.doi.org/10.1167/iovs.10-6856

13. Thibos LN, Wheeler W, Horner D. Power vectors: an application of Fourier analysis to the description and statistical analysis of refractive error. Optom Vis Sci. 1997;74(6):367-75. http://dx.doi.org/10.1097/00006324-199706000-00019

14. Thibos LN, Horner D. Power vector analysis of the optical outcome of refractive surgery. J Cataract Refract Surg. 2001;27:80-5. http://dx.doi.org/10.1016/S0886-3350(00)00797-5

Giuliano de Oliveira Freitas
http://orcid.org/0000-0002-9348-1856
http://lattes.cnpq.br/2229984680546836

Renato Ambrósio Júnior
http://orcid.org/0000-0001-6919-4606
http://lattes.cnpq.br/1789497818458326

Milton Ruiz Alves
http://orcid.org/0000-0001-6759-5289
http://lattes.cnpq.br/6210321951145266

Recebido em: 24 de Agosto de 2016.
Aceito em: 14 de Setembro de 2016.