Harley E. A. Bicas
DOI: 10.17545/eOftalmo/2021.0012
RESUMO
Considera-se a refração em secções de superfícies elípticas para mostrar que com ajustamentos específicos de suas excentricidades se possa prover a condição de “asfericidade” (formação da imagem em um único ponto, o foco imagem da superfície) quando a incidência for a de frentes de ondas planas e com direção paralela ao eixo óptico, isto é, quando o objeto (fonte de energia radiante) estiver à distância infinita. Contrariamente, para objetos situados a distâncias finitas, a “asfericidade” não pode ser assegurada por superfícies elípticas. As formulações e os respectivos cálculos demonstrativos são apresentados. Também se mostra que a multifocalidade, dependente de raios de curvatura variáveis em uma superfície, é condição óptica própria das secções elípticas que servem como matrizes dessas aplicações refratométricas.
Palavras-chave: Refração esférica; Superfícies elípticas; Multifocalidade.
ABSTRACT
Refraction from elliptical surface sections is analyzed in this study. With specific adjustments of their eccentricities, the condition of aspherical refraction (image formation at an only point the focal point of the surface can be achieved when the incident wave exhibits plane wavefronts and propagates parallel to the optical axis, i.e., when the object (radiant power source) is at infinite distance. On the contrary, for objects located at finite distances, elliptical surfaces cannot produce aspherical refraction. The formulations and their respective demonstrative calculations are presented in this study. We also show that multifocality, governed by varying radii of curvature on a surface, is a specific optical condition of elliptical sections which serve as matrices of these refractometric applications.
Keywords: Aspherical refraction; Elliptical surfaces; Multifocality.
INTRODUÇÃO
O estudo da Óptica Geométrica é de suma importância em Oftalmologia, por abordar um de seus aspectos mais utilizados em sua prática diária, a refratometria ocular com as eventuais providências dela decorrentes (prescrição de correções ópticas). Realmente, reconhece-se que as consultas oftalmológicas, em sua grande maioria, ocorrem por problemas que podem ser corrigidos, simplesmente, pela adequada aplicação de providências relacionadas à refração ocular, como lentes de óculos, lentes de contato, lentes intraoculares, remodelagens cirúrgicas da face anterior da córnea e outras intervenções. Assim, nos dois mais importantes livros editados pelo Conselho Brasileiro de Oftalmologia sobre o assunto, é paradigmático o relevo dado ao fenômeno óptico da refração e suas aplicações, já na primeira frase de seus prefácios. O mais antigo1 inicia-se precisamente com a cita de que “A refratometria ocular é o procedimento de maior demanda entre todos os que levam uma pessoa a consulta oftalmológica.” O mais recente2 reassume essa importância reverberando que “Entre as múltiplas ações esperadas de um oftalmologista no exercício de sua profissão, a mais comum é a das prescrições ópticas.”
Obviamente, os conhecimentos sobre a refração não se limitam a tais especialistas, mas se estendem a quem desenvolve os princípios dessas soluções, a quem fabrica ou comercializa os produtos que as possibilitam, mas também interessam a outras áreas da atividade humana, tão diversas quanto as de prospecção visual de objetos muito distantes (telescopia, astronômica ou terrestres) ou muito pequenos (microscopia). De fato, até a relativamente pouco tempo a refração era tida como um fenômeno óptico, ligada à propagação da luz. Hoje, entretanto, sabe-se que ela é mais geral, abrangendo radiações de quaisquer frequências.
Embora não seja um fenômeno exclusivamente óptico, foi com essa conotação que a refração foi primeiramente descrita. Aliás, são surpreendentes as observações empíricas obtidas no século II por Ptolomeu (Klaúdius Ptolemaios, vivido entre os anos 90-168 conforme algumas fontes, ou 100-160, conforme outras) que, com suas medidas de ângulos de refração do ar para a água e do ar para o vidro, atingem notáveis aproximações aos valores exatos, ainda mais quando se pensa na instrumentação relativamente precária da qual ele dispôs para chegar aos resultados. Por exemplo, nas medidas a cada 10° na variação das incidências de 0 a 60°, do ar para a água, seus erros absolutos são de 16,14’ ± 16,48’ (o maior é de 39’, na incidência de 20°); e do ar para o vidro, 17,12’ ± 15,11’ (o maior erro é o de 34’ na incidência de 20°), isto é, de apenas (em média), cerca de 2,08%. (A quase totalidade das diferenças corresponde a que os valores medidos excedem os reais, o que faz pensar em um erro sistemático no processo das mensurações.) Enfim, é bem possível que se Ptolomeu dispusesse do arsenal matemático pelo qual a lei da refração foi depois enunciada, ele teria chegado à sua formulação. Corretamente, postulou que quando a luz (ou os “raios” de visão) passa a um meio com maior índice de refração, aproxima-se da perpendicular à superfície; e, ao contrário, quando passa desse meio a outro, com menor índice de refração (ar), distancia-se daquela perpendicular (Hirschberg, p. 151)3, um princípio que não mais foi alterado.
Mas foi necessária a transcorrência de mais um milênio e meio para que a lei genérica da refração – uma concepção de elegante simplicidade – fosse formulada, um conhecimento que só pôde ser desvendado no século XVII, face ao instrumental matemático necessário para enunciá-la. Ela trata da possível mudança de direções entre a da “incidência” da energia radiante em um meio e a da “refratada” no seguinte, em cada ponto específico de uma superfície que os separa.
Essa descoberta é atribuída a Willebrord Snel van Royen (1580-1626), ou Willebrord Snellius (com dois “l” na transcrição latina de seu nome holandês e pela qual se chegou à versão anglo-saxônica hoje difundida “Snell”) e embora não haja uma data específica para certificá-la, pois foi apenas descoberta após sua morte, entre seus escritos, aparecia como
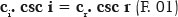
isto é, as cossecantes dos ângulos de incidência (csc i) e de refração (csc r) são inversamente proporcionais às velocidades da luz nesses respectivos meios (ci e cr). A forma canônica, como hoje ela é conhecida, foi proposta por René Descartes (1637),
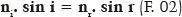
isto é, os senos dos ângulos de incidência (sen i) e de refração (sen r) são inversamente proporcionais aos índices de refração desses respectivos meios. Ora, como a cossecante de um ângulo é a função trigonométrica recíproca do respectivo seno; e como o índice de refração de um meio (por exemplo, o de incidência, ni), corresponde ao valor da velocidade da luz nesse meio (por exemplo, o de incidência, ci) relativamente à velocidade da luz no vácuo (c0), isto é, ni = c0 / ci, ou seja, um valor de magnitude inversa (quanto menor a velocidade da luz no meio, maior o seu índice de refração) há uma absoluta reciprocidade entre as formulações de Snell e de Descartes, consubstanciando a expressão “lei de Snell-Descartes”:
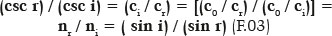
O fenômeno da refração, portanto, é governado por uma lei, cuja formulação é a de uma relação de ângulos (expressos por uma função trigonométrica), constante para o par de meios entre os quais ela ocorre (isto é, a relação entre os seus índices de refração). A questão de como quantificar esses ângulos (o de incidência, i; e o de refração, r) requer, implicitamente, o estabelecimento de uma referência, a linha imaginária, normal (isto é, a perpendicular) ao ponto onde a refração ocorre.
Em geometria, não há sentido em se falar em linha perpendicular a um ponto (infinitas linha retas, em quaisquer direções, podem passar por um ponto). Para solucionar essa questão, considera-se que o ponto sobre o qual a refração ocorre é o lugar de coincidência da superfície (que o contém) e da tangente que por aí passa. Assim, uma perpendicular à tangente à superfície, nesse ponto, é, igualmente, perpendicular à superfície. Em outras palavras, entre as infinitas linhas que poderiam servir como referência, apenas uma toma-se como válida, a linha “normal” à superfície (passando pelo ponto). Portanto, embora a refração seja, efetivamente, um fenômeno “pontual”, ela depende da curvatura da superfície no ponto onde a refração ocorre.
Em outras palavras, a afirmação de que a refração sobre um ponto independa da superfície é correta apenas parcialmente. De fato, a asserção é verdadeira em sua essência: a direção tomada por um “raio” (direção da frente de ondas com que se propaga a energia radiante) é a mesma, quer a superfície seja plana, côncava, convexa, ou de qualquer outra forma (Figura 1). Mas, ainda que o raio refratado siga na mesma direção, independentemente da forma da superfície, a afirmação não é válida para uma das principais aplicações práticas da Óptica, a posição da imagem de um objeto (Figura 1).
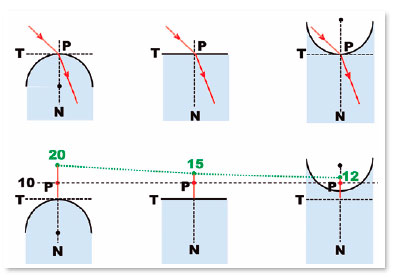
Por exemplo, para um objeto situado à distância p = –10 cm, supondo-se os raios de curvatura das superfícies convexa (R = +20), plana (R =±∞) ou côncava (R = –20), as respectivas imagens formar-se-ão às distâncias q = -20 cm, q = -15 cm e q = -12 cm, isto é, em posições diferentes relativamente a cada uma das superfícies, dependentes das respectivas curvaturas no ponto considerado. (Se o objeto estiver a –100 cm, as posições das imagens serão, respectivamente a +100 cm, -150 cm e -42,86 cm).
Curvatura de uma superfície
Ainda que a refração seja postulada como ocorrendo em um “ponto” –uma definição “axiomática” na Geometria euclidiana, mas que não se aplica ao estudo da refração, pois, como já comentado, ela se refere a uma direção, por sua vez relacionada à respectiva “perpendicular” ao ponto considerado, – o correto é mencionar-se que ele pertença a uma superfície (no espaço tridimensional), ou uma sua secção, ou linha (no bidimensional). Em outras palavras, o tratamento de uma perpendicular a um ponto de uma superfície (ou linha), subordina-se ao conceito de curvatura da superfície (ou linha) naquele ponto considerado e se quantifica pelo “comprimento” dessa perpendicular, isto é, pelo chamado raio de curvatura da superfície (ou linha), naquele ponto específico. Enfim, o conceito da refração é intimamente dependente do de curvatura da superfície (ou linha) em um de seus pontos.
Linhas, ou superfícies, podem ser matematicamente definidas por suas curvaturas, ou por seus recíprocos raios de curvatura: ou constante e infinito (o de uma reta, ou o de um plano), ou constantes e finitos (os de círculos, ou esferas), ou progressivamente variáveis (e.g., os de secções cônicas, esferoides, ou elipsoides), ou, ainda, de outras naturezas. A refração em superfícies planas tem larga aplicação no estudo dos prismas ópticos. Já as lentes oftálmicas de correções de defeitos da óptica ocular são todas, curvas (em pelo menos uma de suas faces), e é estranho que embora os fundamentos de suas refrações sejam explicitados pelo que ocorre em superfícies esféricas (pela relativa simplicidade de seus desenvolvimentos) apenas a elas se limitem. Além disso, conquanto se reconheça que essa óptica (a de superfícies esféricas) seja, inerentemente, “defeituosa” (pelo chamado fenômeno da aberração da esfericidade) é muito pouco provável encontrar-se que tanto a solução desse problema (a da óptica de lentes esféricas, isto é, sem a aberração da esfericidade) quanto a de refinamentos ópticos, como o das lentes multifocais possa ser o de superfícies elípticas.
Em verdade, o estudo minucioso de curvaturas impõe grandes dificuldades, como a de exigir o conhecimento da chamada Geometria Diferencial. Mas em certos casos mais simples, como o da refração em superfícies elípticas, o tratamento analítico cartesiano dos problemas é suficiente. Mesmo assim, é notório o desconforto desses caminhos, como sabiamente exposto na apresentação de outro livro texto nacional muito festejado4, em menção a outra incontestável referência pedagógica sobre o estudo da refração5: “fortunately Donders was-self – admittedly – no mathematician and he wrote in clear and simple language, so that his book became popular.” E, em subsequente complementação, a outra obra “clássica” 6: “O mestre britânico... (Duke-Elder)...publicou um livro, ‘The Practice of Refraction’ (1ª Edição, em 1928), no qual procurou evitar uma apresentação matemática dos erros da refração e do modo de corrigi-lo...4.
Inequivocamente, desenvolvimentos matemáticos são, em geral, de difícil acompanhamento quando não se lhes tem familiaridade, mas imprescindíveis a quem pretenda aprofundamentos em assunto ao qual eles dão fundamento (e o celebérrimo Helmholtz, em seu celebérrimo Tratado de Óptica Fisiológica, em três volumes – ao qual se voltará, adiante – usou e abusou desse recurso). Isso não justifica que, pelo menos, falte a referência, à natureza da solução do problema. Assim mostra-se absolutamente desconcertante que nem sequer apareça a menção aos termos “elipse” e ”curva (ou superfície) elíptica”, ou similares e correlatos relacionados à óptica apresentada, quer nos livros recomendados ao estudo da refração já citados1-6, quer em outros7-10, ou em dedicados a ópticos (fabricação de lentes)11,12, ou nos internacionais mais conhecidos, antigos e recentes13-25. Quando esses termos aparecem, não têm a ver com o fenômeno da refração em sua própria natureza; por exemplo, elipse de Tscherning24 (a expressão gráfica da relação entre o poder dióptrico de lentes oftálmicas e as chamadas curvas base recomendadas) ou polarização elíptica19 (por relação a uma das modalidades do fenômeno da polarização da energia eletromagnética). De fato, mesmo quando as secções elípticas são consideradas, como é o caso das seções de lentes cilíndricas (ou tóricas) inclinadas relativamente aos seus eixos, não se aborda a óptica própria das secções elípticas. Aliás, em um dos mais importantes compêndios de Oftalmologia26, le-se que: “The surface dealt with in optics are generally spherical in shape... while the production of non-spherical or aspheric surfaces (which are actually more desirable in some instances) is extremely difficult. For this reason, spherical surfaces are employed almost exclusively in optics, and they usually perform adequately” (pp. 6-7)26. E mesmo quando abordando as lentes cilíndricas, a menção a “elípticas” (para suas secções) não aparece. Ao contrário, a pouca familiaridade com essas questões geométricas elementares, leva à surpreendente afirmação de que “There is no optical power in oblique meridians of a toric refracting surface” (p. 46, op. cit.). O erro foi o de não considerar a coplanaridade dos raios incidentes e refratados, mas “...’skew rays’ because they are skewed about the axis”, com que o texto conclui: “these limiting rays are deviated by different amounts in the two corresponding directions.” (O grifo é meu.) Em edição posterior27 essa impropriedade é corrigida, admitindo-se que “There is a diferent power in every meridian” (p. 87), o que é ilustrado por uma figura elucidativa (fig. 72), mas também não se entra em pormenores sobre como e porque essa refração (em superfícies elípticas) possa ocorrer.
A propósito, no reverenciado e profundo tratado de Óptica Fisiológica de Helmholtz, há a referência a “elipsoidal refracting surface” (volume I, p. 194)13, mas o conteúdo dela subordina-se às aberrações que ocorrem na refração pela superfície de um elipsoide (como a de uma córnea astigmática), descrevendo a figura geométrica que modernamente se conhece como o “conoide de Sturm”. Aliás, Helmholtz registra a devida referência creditícia a esse autor no capítulo anterior do mesmo volume, mas seguida de sua observação corretiva14: “Aberrations of the kind that STURM supposes actually do seem to occur in most human eyes, and the phenomena dependent on them will be described; where, however it will be shown that the interval between the two focal planes is by no means so important as STURM thinks and that, instead of promoting the clearness of vision, this defect in the eye tends rather to impair it.” Ressalte-se que até, também, Allvar Gullstrand – Prêmio Nobel de Fisiologia ou Medicina em 1911, justamente por seus estudos sobre a dióptrica ocular – convidado a rever essa monumental obra de Helmholtz e a enriquecer com a inserção de suas percucientes notas e apêndices, não se detém sobre o assunto, nem menciona elipses e suas ópticas28.
Em suma, a falta de referências explícitas sobre a refração em superfícies elípticas, parece justificar que se as apresente suscintamente, para, eventualmente despertar interesses em seus aprofundamentos.
Refração em uma superfície esférica
Uma esfera representa grande simplicidade no estudo da refração, por ter uma curvatura constante em quaisquer de seus pontos, isto é, um único centro sobre o qual passam todas as linhas normais a quaisquer tangentes de sua superfície. As secções planas de uma esfera são círculos de diferentes raios de curvatura, cujo valor máximo corresponde ao do diâmetro equatorial.
O fato de haver apenas um centro (C) permite que se relacione, relativamente a essa superfície, a medida de seu único raio de curvatura (R), a distâncias dela a um ponto objeto (p) e a de sua respectiva imagem, em função do ângulo de incidência (i). Lembre-se que pelo fato de se considerar um ponto objeto, qualquer que seja sua posição no espaço relativamente à superfície esférica, ele pode ser, sempre, considerado como estando sobre uma mesma linha que contenha o centro de curvatura dela, isto é, sobre o eixo óptico respectivo. De fato, pela figura 2, aplicando-se a lei dos senos aos triângulos OPC e CIP, resulta, respectivamente:

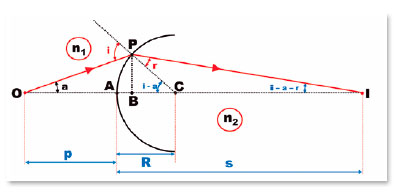
Essa representação geométrica (F. 04) pode ser transformada nas variáveis de seus respectivos significados, isto é, as distâncias p, s e R e nas coordenadas do ponto P, já que
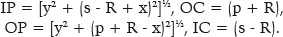
Portanto, (nr / ni) =
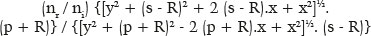
Mas, como, pela equação dos círculos, x2 + y2 = R2; vem:
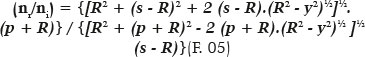
ou seja, dados os valores das variáveis y (“altura” do ponto de incidência, relativamente ao eixo óptico) e R (raio de curvatura da superfície), chega-se a uma equação de segundo grau para o cálculo de s (em função de p), ou de p (em função de s).
De qualquer modo, por sua própria extensão, essa formulação, embora genérica, é evitada. Em seu lugar, prefere-se a que se denomina “equação dos raios paraxiais”, cujo significado é o de um valor tão pequeno do ângulo de incidência (“rasante” ao eixo óptico) que ele possa ser negligenciado. De fato, fazendo-se y = 0, vem:
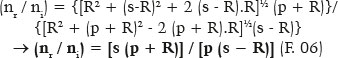
Aliás, ainda mais difundida é a fórmula que resulta de um desenvolvimento da acima apresentada.
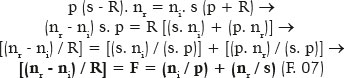
O valor de F é assumido como o do poder focal da superfície, sendo expresso na unidade óptica “dioptria” (símbolo “D”) quando o valor do raio de curvatura (R) for quantificado em metros. Ele é constante para cada superfície esférica, pois depende de valores invariáveis: o do raio de curvatura da superfície (R) e os dos índices de refração dos meios por ela separados (ni, o de incidência; e nr, o de refração).
Outra simplificação da fórmula genérica (F.05) é a de se considerar o posicionamento do objeto a uma distância infinita. Daí:
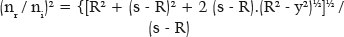
uma equação quadrática para o valor de (s – R), dependente da variável y. Resolvendo-se a equação de segundo grau:
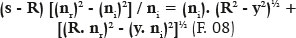
E como, neste caso, y = R sen i:
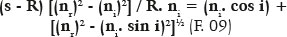
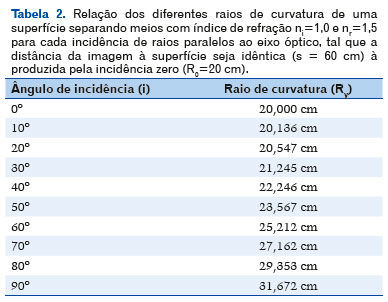
Essa fórmula é muito importante, por mostrar que raios paralelos ao eixo óptico (isto é, provindos de uma distância infinita), atingindo a superfície em diferentes alturas relativamente ao eixo óptico (y) e, ou, com diferentes valores do ângulo de incidência (i), darão imagens a diferentes distâncias (s) da superfície, isto é, com a chamada aberração esférica longitudinal. Por exemplo, para nr = 1,5, ni = 1,0, R = 20 cm, os valores de s, em função dos de y são mostrados na tabela 1:
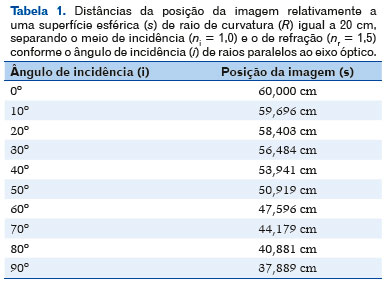
Em outras palavras, a energia que atinge a superfície não se concentra sobre um único ponto (foco) e se dispersa, por um espaço cujos limites são contidos por uma superfície denominada cáustica (Figura 3).
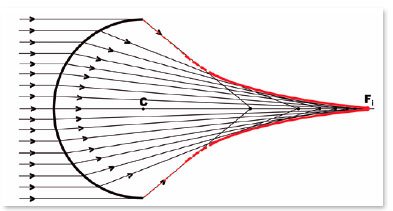
Superfícies asféricas
A indesejável condição da aberração esférica suscita a conveniência de se buscar outra superfície que possa concentrar como energia refratada em um único ponto (o chamado ponto focal imagem, o da distância da imagem de um objeto situado sobre o eixo óptico e a distância infinita; no exemplo da tabela 1, s = 60 cm), toda a energia incidente sobre a superfície. Isso equivale a buscar superfícies cujos raios de curvatura sejam progressivamente maiores, isto é, curvaturas menos acentuadas. Em outras palavras, buscar para cada altura relativamente ao eixo óptico (y) o raio de curvatura específica (Ry), para que a imagem do objeto se forme coincidentemente sobre imagem correspondente à incidência i = 0°.
É então o caso de se voltar mesma F. 09, mas trocando o que se busca como variável, não mais a da posição da imagem (s) em função de um raio de curvatura constante (R0 = 20 cm, tabela 1), mas, ao contrário, o valor do raio de curvatura (Ry) para que se obtenha a imagem sempre na mesma posição (s = 60 cm, Tabela 2). Para facilitar o cálculo de R em função das demais varáveis, a F. 09 deve ser rearranjada para:
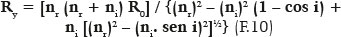
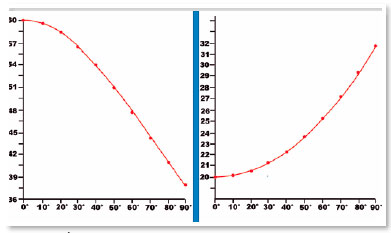
A figura 4 é apresentação gráfica das tabelas 1 e 2, ilustrando a variação da posição da imagem, conforme a altura relativamente ao eixo óptico em que se dá a incidência de um raio que lhe é paralelo (Figura 4 a) e, reciprocamente, a variação do raio de curvatura para que a imagem se forme, sempre, sobre um mesmo ponto (Figura 4 b).
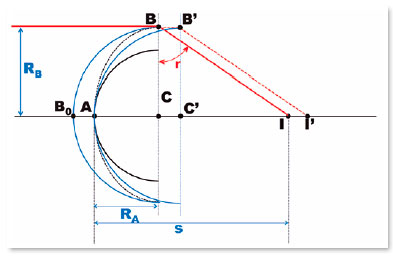
A concepção pela qual a tabela 2 foi construída suscita reparos, conforme a figura 5 esclarece. De fato, a distância a que se forma a imagem de uma incidência nula (i = 0°) formada pela superfície com centro C e raio de curvatura AC = RA é AI = s. Uma superfície de maior raio de curvatura, RB = BC, com o mesmo centro da superfície A, forma a imagem para a incidência i = 90° no mesmo local (I). Entretanto, para que isso ocorra, seu ápice (a posição em que a superfície é cortada pelo eixo óptico) estará em B0, local não concordante com o do ápice da superfície anterior que gerou a primeira imagem (A) Se houvesse concordância desses ápices (em A), a curva dessa superfície descreveria o arco AB’, seu centro de curvatura não seria C, mas C’ e a posição da imagem estaria em I’ (Figura 5). Assim, para que os ápices coincidam (em A), tanto quanto os centros de curvatura (em C), o desenho de curvas com imagens formadas no mesmo local (I), sem a chamada “aberração esférica”, deve seguir outra curva (linha interrompida entre A e B na Figura 5).
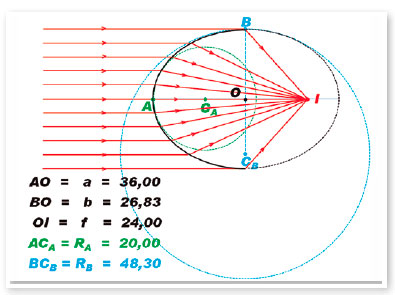
Na verdade, existem várias curvas com progressões crescentes, ou decrescentes, dos raios de curvatura em cada um de seus pontos, sendo as elipses as que possibilitam, no fenômeno da refração, a condição de ajustamento de variáveis (índices de refração entre os meios separados pela superfície e progressão dos raios de curvatura) para que os raios refratados se formem, sempre, em um mesmo ponto “focal” (Figura 6).
Aliás, ao contrário das superfícies esféricas em que aparece, na refração, a aberração da esfericidade, precisamente porque, nelas, o raio de curvatura é constante, nas superfícies elípticas se pode observar uma progressão crescente ou decrescente desses raios de curvatura (Figura 7), determinando, seja uma acentuação daquelas aberrações, seja reduzindo-as até anulá-las e invertê-las. Assim, uma única e específica forma (para cada par de meios ópticos separados pela superfície) é a que se relaciona à condição de não aberração da esfericidade, embora, rigorosamente, todas elas sejam “asféricas”, isto é, “não esféricas” (Figura 8).
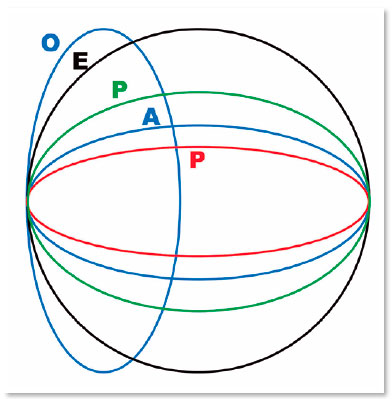
Uma das características distintivas das elipses e que as caracterizam matematicamente é a sua excentricidade, um valor que corresponde à sua deformação relativamente ao círculo. (A excentricidade do círculo é zero.) Entretanto, não se pode associar, diretamente, a excentricidade de uma elipse ao tipo de aberração, pois a mesma elipse (portanto mesma excentricidade) pode ser relacionada ao eixo óptico de vários modos. De fato, as elipses O e A (Figuras 7 e 8) são idênticas em suas excentricidades, mas diferem quando se relacionam ao eixo óptico, com o maior de seus eixos no plano horizontal (curva A) ou com o menor (curva O), cujos efeitos sobre a refração são completamente diferentes. Note-se que com o raio de curvatura do ponto apical horizontal, acontece o inverso: o menor raio de curvatura é o da curva A e o maior é o da O.
A questão semântica da asfericidade
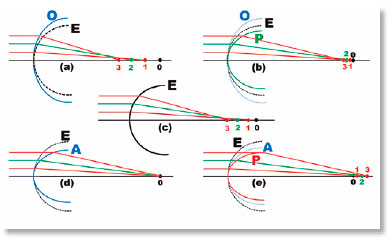
Obviamente, seja por variações crescentes dos raios de curvatura, ou decrescentes, as curvas resultantes são todas “não esféricas”, ou “asféricas”, ou anesféricas. Do ponto de vista da aberração refracional pela forma da superfície, todas, também, a produzem, com exceção de uma única. Ou seja, o que caracteriza essa superfície especial da Óptica Geométrica é a sua “não-aberração”, uma “inaberração”, não sua forma própria. Assim, as denominações mais adequadas para definir o tipo de aberração suscitada (tomando-se como referência a aberração “esférica”), são as de superaberração (positiva) quando essa aberração estiver majorada (curva O, Figura 8 a), a de subaberração, quando ela for reduzida (P, Figura 8 b), a de inaberração quando ela não estiver presente (curva A, Figura 8 d) e a de contraberração (negativa), quando ela se inverter de sentido (curva P, Figura 8 e). Vê-se que as curvas oblatas serão, sempre, superaberrantes, mas com as prolatas podem ser encontradas as aberrações esféricas reduzidas (Figura 8 b), ou nulas (Figura 8 d), ou invertidas (Figura 8 e). Não há, pois, razão para se dizer que a superfície inaberrante seja prolata, pois embora isso seja verdadeiro, representa um caso particular: nem toda curva prolata é inaberrante.
A geometria das elipses
Outros elementos da geometria da elipse deixaram de ser mostrados na figura 9 para não sobrecarregá-la, mas são apresentados na figura 10.
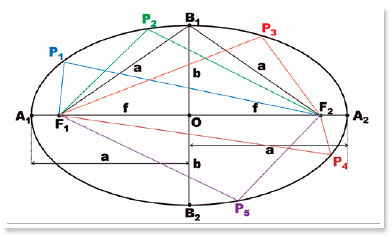
Como, nas elipses, a distância entre B1 (ou B2) e um dos focos (G ou Q) é igual ao comprimento do semieixo maior (a), uma relação entre as variáveis a, b e f fica evidente:
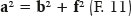
A equação canônica da elipse, a que relaciona as coordenadas cartesianas de um de seus pontos, P (x,y), relativamente à origem do sistema de medidas (simplificadamente tomado como o centro da elipse), pode ser deduzida a partir dos elementos da figura 9:
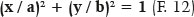
Outra relação é a que define a excentricidade da elipse (e):
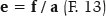
Aliás, esse valor serve como distinção das chamadas secções cônicas, a saber:
a) O círculo (e = 0), obtido pela secção plana do cone perpendicular a seu eixo principal.
b) A elipse (1 > e > 0), obtida pela secção plana do cone inclinada relativamente a seu eixo principal, mas atravessando-o.
c) A parábola (e = 1), obtida pela secção plana do cone, paralelamente a uma de suas geratrizes (as linhas que vão do ápice à base).
d) A(s) hipérbole(s) (e >1), obtida(s) pela secção plana do cone paralela ou inclinada a seu eixo principal, mas sem atravessá-lo.
A relação das coordenadas cartesianas de um ponto P (x,y) em um sistema cuja origem seja o centro da elipse O (0,0) é dada por:
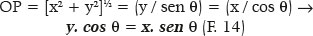
Por substituição de y da F. 14 na equação canônica da elipse (F. 12), escrita de outro modo:
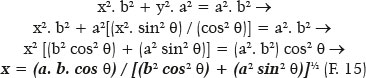
E, analogamente:
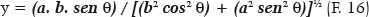
E, pois, a distância do ponto considerado (P) ao centro da elipse (O), isto é, a distância OP, é dada por:
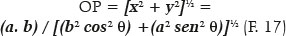
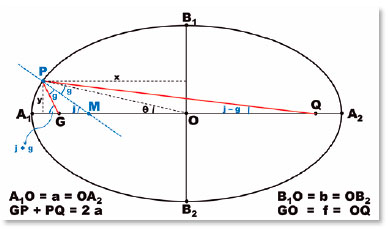
Uma condição muito importante é a de que a normal a cada ponto da elipse (isto é, a linha perpendicular à tangente da elipse naquele ponto) é a bissetriz do ângulo entre as linhas entre ele (P, Figura 10) e os focos da elipse (G e Q). Essa linha (PM, Figura 10) define relações angulares (j e g, no triângulo GPM), pelas quais os ângulos de incidência (i) e de refração (r) em um ponto da superfície serão, adiante, considerados.
Daí, podem ser estabelecidas as relações, nos triângulos GPM e MPQ:

Há vários desenvolvimentos que podem ser daí originados. Mas lembrando-se que:
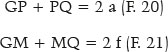
consideremos (da F. 18, para o valor de GM e da F. 19, para o de MQ):

O conjunto (1 – e2) = k pode ser útil como simplificação de equações, como se verá a seguir. De qualquer modo, a F. 23 traz a resposta do valor de j em função do de PM (ou vice-versa). Mas, como sen j = y / PM, vem:
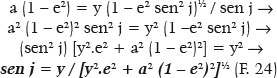
e, pois:
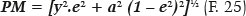
A equação F. 17 (e, similarmente, a F. 15 e a F. 16) pode ser reescrita em função de k = 1 – e2:
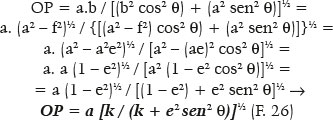
A equação do raio de curvatura em um dos pontos P da superfície (RP) é:
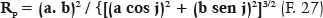
de onde se conclui que, para um dos vértices do eixo maior (j = 0°):
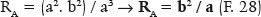
enquanto para um dos vértices do eixo menor (j = 90°):
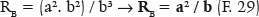
Enquanto a localização do centro de curvatura relacionado a cada um dos pontos da superfície será objeto de considerações posteriores, já se podem exemplificar as relações sobre a refração de uma curva sem a aberração da esfericidade.
A refração em uma superfície sem aberração esférica
Considere-se um ponto objeto situado a distância infinita de uma superfície que separe dois meios, o de incidência e o de refração, com índices de refração ni e nr, respectivamente (sendo nr> ni). Considere-se “A” um ponto dessa superfície em que ocorra a incidência da radiação e seja q uma distância finita, tomada a partir dele (“A”) em que se forme a imagem (Q) do objeto situado à distância infinita. Isso significa que a superfície então considerada seja curva (pois para uma superfície plana, de raio de curvatura infinito, a imagem Q de um objeto a distância infinita formar-se-ia, também, a distância infinita). Independentemente da forma dessa superfície (esférica, elíptica, ou outra qualquer), o cálculo da posição da imagem (Q) é dado pela assunção de que se possa atribuir um raio de curvatura a esse ponto “A” da superfície, equivalente ao de uma superfície esférica, como sugerido pela figura 6.
Seja “RA” o raio de curvatura nesse ponto (A) da superfície. Pela fórmula da refração em uma superfície esférica, a relação entre a posição da imagem, relativamente a A (isto é, q) e o raio de curvatura (RA) pode ser estabelecida em função dos respectivos índices de refração (ni e nr) como:
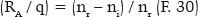
que pode ser reescrita em função do poder focal atribuído à superfície (F):
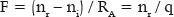
Portanto:
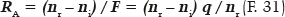
A condição de não aberração esférica dessa superfície pressupõe que um ponto P (qualquer) dessa superfície tenha a imagem do objeto (situado a distância infinita) formada exatamente sobre Q, isto é, coincidentemente a ele. A direção da incidência da radiação sobre P é, pois, paralela à direção da incidência sobre o ponto A. Pela normal ao ponto P e (ainda) independentemente da forma da superfície, as relações geométricas dessa coincidência podem ser estabelecidas (Figura 11).
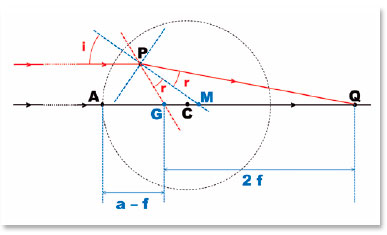
Pela hipótese de que G e Q sejam os focos de uma elipse à qual pertença P, valerão, para os triângulos GPM e MPQ, respectivamente, as relações:
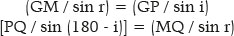
Portanto:
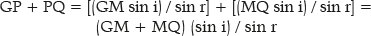
Mas, em uma elipse, GP + PQ = 2 a, isto é, a soma das distâncias do ponto considerado, P, a cada foco (G e Q) é igual ao comprimento do eixo maior da elipse; e GM + MQ = 2 f. Assim:
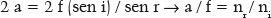
E como (f / a) = e, é a medida da excentricidade da elipse, fica estabelecida a relação fundamental entre a “forma” dela (dada por sua excentricidade, e) e a relação entre os índices de refração dos meios considerados, para que a incidência de raios paralelos sobre quaisquer pontos dessa superfície (isto é, todos) produza raios refratados que convirjam a um único ponto (Q), um dos focos da elipse:
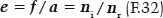
Em outras palavras, para que uma curva não tenha aberração esférica, ela deve ser elíptica e com uma excentricidade tal que corresponda à relação dos índices de refração dos meios de incidência e de refração por ela separados.
Satisfeita essa condição, infinitas superfícies podem existir, cada uma com a distância focal (AQ = q) específica, a qual é função do raio de curvatura do ponto apical do eixo maior (A), isto é, RA, cujo valor já foi definido (F. 30 e F. 31). Assim, na Figura 11, como AG = a – f, a distância focal, genericamente formulada, é:
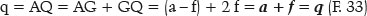
Enfim, as variáveis da elipse podem ser determinadas em função de q (distância focal imagem) ou de F (poder focal da superfície), convencionalmente tomados em função do raio de curvatura do ponto apical do eixo maior da elipse considerada (RA). Assim, para o comprimento do semieixo maior da curva (elipse), a:

Outras relações, entre essas variáveis podem também ser obtidas (por exemplo, a – f, a / b, etc. A tabela 3 resume essas formulações para a superfície sem aberração esférica.
Algumas relações são puramente dependentes da própria elipse, tais como a da excentricidade (e) que a define, ou outras que podem ser deduzidas das fórmulas já apresentadas:
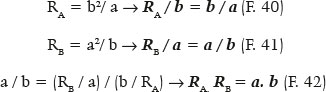
Tome-se como exemplo numérico uma superfície que separe meios, cujos índices de refração sejam 1,0 para o de incidência (ni = 1,0) e 1,5 para o de refração (nr = 1,5). Essa informação já enseja a determinação de qual deva ser a excentricidade da curva (elíptica) tal que ela não produza aberração esférica, isto é, e = ni/nr = 1,0/1,5 = 0,666... Seja o raio de curvatura no ponto apical de seu eixo maior igual a 20 cm (RA = 20 cm). O poder focal dessa superfície (objeto situado a distância infinita da superfície) é F = (1,5 – 1,0)/0,2 m = 2,5 D. A distância focal imagem dessa superfície é q = 1,5 / F = 1,5 / 2,5 = 0,6 m = 60 cm. Nessa curva, o semieixo maior (a) é, então (cálculo que pode ser feito, alternativamente, ou a partir de q = 60 cm, ou de RA = 20 cm, ou de F = 2,5 D), a = 36 cm (ou 0,36 m, se o cálculo for feito pela fórmula que contenha o valor de F). O semieixo focal é f = 24 cm. O semieixo menor é b = 720½ cm ≈ 26,833 cm e o raio de curvatura do ponto apical do eixo menor é RB ≈ 48,299 cm. De fato, supondo-se um raio incidente paralelo ao eixo óptico e tangenciando esse ponto apical do eixo menor (uma conjetura puramente matemática), vem, pela lei de Snell:
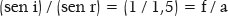
pois f = 24 cm e a = 36 cm, exprimindo a relação de excentricidade dessa curva. E, obviamente, (a –f) = 12 cm, cujo cálculo é confirmado por quaisquer das fórmulas apresentadas pela tabela 3, referentes a essa variável (a- f).
A tabela 4 resume valores das variáveis de curvas sem aberração esférica, conforme o índice de refração nr, para o caso de o de incidência (ni) ser o ar (ni = 1,0).Os cálculos do exemplo acima considerado (q = 60 cm e Figura 12) correspondem aos da terceira linha da tabela 4 (nr = 1,500).
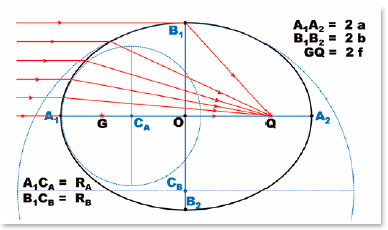
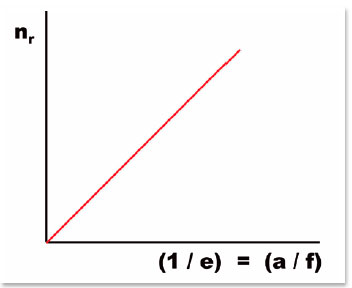
Uma relação muito importante é a da excentricidade da curva, para que ela não apresente aberração da esfericidade, quando o meio de incidência for o ar. Nesse caso, ni = 1,0 e a expressão da excentricidade se expressa pelo inverso do índice de refração do meio de refração (nr, isto é, e = 1/nr). Ou, reciprocamente, e-1 = nr = a / f. Essa é uma simplificação interessante, por mostrar a perfeita linearidade entre o índice de refração nr e a relação entre os comprimentos do eixo maior (2 a) e da distância interfocal (2 f) da superfície sem a aberração esférica (Figura 13).
O posicionamento do centro de curvatura
1) Para se determinar, graficamente, a posição do centro de curvatura de qualquer ponto de uma superfície elíptica os procedimentos são os de (Figura 14):
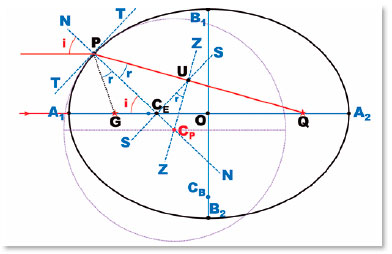
2) Traçar a linha tangente (TT) ao ponto da superfície (P) cujo centro de curvatura se deseja determinar;
3) Traçar a linha normal, NN (que conterá o centro de curvatura do ponto P), perpendicular à tangente à superfície (TT) no ponto considerado (P).
4) No ponto de cruzamento da linha normal (NN) com o eixo maior da elipse (A1A2), define-se um ponto (M), pelo qual se traça uma linha paralela à tangente TT, isto é, a linha SS.
5) Do ponto de cruzamento da linha SS com a linha que une o ponto (P) ao foco mais distante (Q), linha PQ, isto é, o ponto U, traça-se uma perpendicular à direção PQ (a que se considera ser a do raio refratado), a linha ZZ.
6) No cruzamento da linha ZZ com a normal ao ponto P (linha NN), localiza-se o centro do círculo osculador ao ponto P (ponto CP) sendo PCP = RP o raio de curvatura desse círculo.
A figura 15 é a reprodução da Figura 14, depurada dos elementos que serviram para a construção do ponto CP. Ela facilita a compreensão da dedução geométrica que se segue.
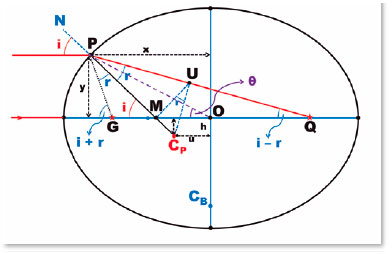
As coordenadas do ponto P e CP são, respectivamente, P (x, y) e CP (u, h). Daí vem a determinação do raio de curvatura (RP):
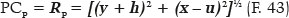
As relações entre as funções da curva elíptica (a, b, f, RA), as coordenadas de um de seus pontos (x, y, θ) e as respectivas funções relacionadas a refração (i, r, ni, nr, q, F, etc.) são obtidas a partir das seguintes formulações:
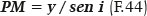
Do triângulo PGM, pela lei dos senos:
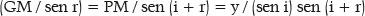
Do triângulos MPQ, pela lei dos senos:
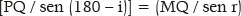
Mas:
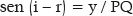
Portanto:
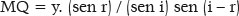
E, finalmente, como GM + MQ = 2 f, vem:
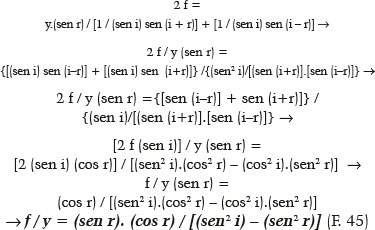
como (f / a) = (sen r) / (sen i), vem:
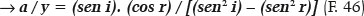
Alternativamente, a equação pode ser convertida para o cálculo de i (ou de r) em função dos valores de y e de a (ou de f, ou de θ, etc.). Assim, da F. 45:
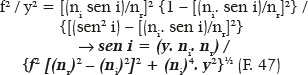
Por exemplo, para os valores nr = 1,5; ni = 1,0; f = 24 cm e tomando-se o caso de y para θ = 40° (pela F. 29, sendo a = 36 cm e b = 720½ cm, vem y = 20,06115396 cm), daí resulta sen i = 1,5 y / (900 + y2) e, pois, i = 56,49204167°. (Note-se que esse resultado pode ser, igualmente, obtido da F. 24, quando j = i.)
O valor do raio de curvatura “aparente” (PM = RM, Figura 15 e F. 44) pode então ser calculado, valendo PM = RM = 20,06115396 / sen 56,49204167° = 24,05964716 cm (resultado também idêntico ao obtido pela F. 25). O do raio de curvatura verdadeiro (PCP = RP) é facilmente calculado dos triângulos PUCP e PMU, respectivamente:
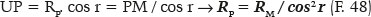
de onde vem RP = 34,81831666 cm.
Daí, os valores das coordenadas do centro de curvatura (u e h):
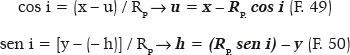
A tabela 5 mostra os valores aproximados (até a terceira casa decimal) dos valores das coordenadas de um ponto P (x, y) em função do ângulo (θ), os da linha (OP) entre esse ponto (P) e o centro da elipse (O), os das coordenadas do centro de curvatura (u e h), o valor do raio de curvatura “aparente” (PM = RM) e do verdadeiro (RP) e os valores dos ângulos de incidência (i) e de refração (r) correspondentes aos pontos cujas coordenadas são consideradas.
A tabela 6 complementa a tabela 5, mostrando (na penúltima coluna) valores da coordenada (m,0) do ponto M, isto é do “pseudo” centro de curvatura do ponto P, ou seja, do local em que a normal a esse ponto cruza o eixo maior da curva (seu eixo óptico principal), gerados pela equação:
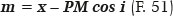
ou de sua respectiva distância ao ponto apical anterior (isto é, a distância A1M = Rm, Figura 14). Note-se que Rm corresponde ao valor do verdadeiro raio de curvatura, quando i = 0° (Rm = RA) e ao valor Rm = PM cos i, quando 90° > i > 0°. De fato, para esses casos m + Rm = x.
Mostra, também, algumas variáveis de apoio a outros eventuais cálculos, assim como o de suas relações. De fato, em certos casos, pode vir a ser de interesse o valor da distância de cada foco ao ponto de P (onde ocorre a incidência e a refração), isto é, GP = d1 e QP = d2 (Figuras 14 e 15), o resultado de sua soma (sempre igual ao eixo maior da elipse, isto é, d1 + d2 = 2 a = 72,000 cm, no exemplo considerado) e de sua razão (d2/d1), aliás, igual à razão entre os senos da soma e da diferença dos ângulos de incidência (i) e de refração (r), conforme dedutível da figura 15:
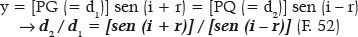
E, finalmente, contempla o valor de s que, como necessariamente esperado, deve corresponder à distância A1Q (Figura 14), a do comprimento focal imagem da superfície considerada:
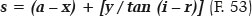
Por exemplo, para θ = 40°, os valores correspondentes são (na Tabela 6): x = 23,908 cm, y = 20,061 cm, (i – r) = 22,721°, de onde resulta s = 60,000 cm.
A excentricidade da curva de não aberração esférica como contingência da posição do objeto
A circunstância de que a excentricidade de uma curva elíptica justifique a ausência de aberração esférica na refração da imagem por ela formada a partir de raios incidentes paralelos ao eixo óptico, não significa que essa propriedade se aplique a outras incidências, isto é, a outras posições do objeto relativamente a essa superfície. De fato, se um objeto situado a distância infinita forma uma imagem a 60 cm da superfície, como foi exemplificado, isso corresponde a um raio de curvatura apical anterior da superfície (RA) igual a 20 cm, do que resultam condicionadas todas as variáveis geométricas da curva (a = 36 cm, f = 24 cm, b = 720½ cm, cujas relações são tipificadas pela excentricidade e = 0,666...como ficou demonstrado para os meios com índices de refração ni = 1,0 e nr = 1,5). Entretanto, um objeto a qualquer outra distância desse ponto apical formará sua imagem, necessariamente, em obediência às leis da refração, a diferentes distâncias, conforme as expressões F. 06 ou F. 07.
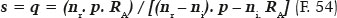
Assim, por exemplo, para as condições já pré-estabelecidas para a superfície sem aberração esférica de raio de curvatura apical RA = 20 cm, nr = 1,5 e ni = 1,0, vem, para p = 120 cm, q = 90 cm. Na mesma superfície elíptica já considerada para exemplificação, a incidência de outro raio desse objeto a outros pontos dela (como P, Figura 16) conduz às relações algébricas, que possibilitam o cálculo da distância s em que se forma a imagem.
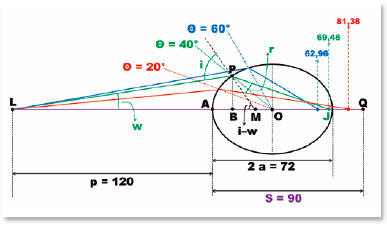
Para o triângulo LBP, sendo LA = p, AB = (AO – BO) = (a – x), PB = y (tomado do valor de θ = 40°), determina-se o valor do ângulo w:
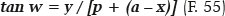
Daí se obtém w = 8,636 cm. Para determinação da direção do raio refratado (ângulo r), requer-se o valor do ângulo de incidência (i), que pode ser determinado a partir da inclinação do raio de curvatura aparente (PM = RM) ou verdadeiro (RP) relativamente ao eixo maior da elipse, isto é, i – w: O raio de curvatura aparente do ponto P é PM = RM, conhecido. Portanto:
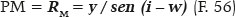
Do que resulta (i – w) = 56,492°, portanto i = 65,128° de onde, pela lei de Snell, vem r = 37,217°. Em seguida, calcula-se BQ:
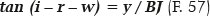
Daí resulta tan 19,275° = 20,061 / BJ, portanto BJ = 57,365 cm. Finalmente, para a incógnita desejada, s = AJ = AB + BJ, vem:
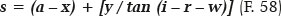
ou seja, s = 12,092 + 57,365 = 69,457 cm. Para outros valores de y (correspondentes a outros valores da coordenada θ, supostamente conhecida), os cálculos são análogos, levando aos valores mostrados na figura 16.
Em suma, a curva cuja forma (excentricidade) seja adequada para anular a aberração da esfericidade das imagens de um objeto situado a distância infinita, não é suficiente para manter essa propriedade (“asfericidade”) se o objeto estiver a uma distância finita. Nesse caso, uma curva de excentricidade maior seria necessária. Em outras palavras, a “asfericidade” (que pode ser definida pelo valor da excentricidade da curva) não é específica para qualquer distância. Ou, ainda, a chamada aberração da esfericidade não se deve ao fato de a superfície considerada ser esférica, mas é uma propriedade inerente à própria natureza da refração.
Portanto, a denominação de aberração da esfericidade é absolutamente imprópria, pois embora ocorra em superfícies esféricas, ocorre, igualmente, em superfícies elípticas que anulam a aberração da esfericidade para a posição do objeto a uma determinada distância (por exemplo, a distância infinita, para a qual se costuma definir a qualidade de uma curva como “asférica”). Mais conveniente é chamá-la por aberração da superfície ou da curvatura da superfície. (Aberração da curvatura, simplesmente, pode induzir confusão com as aberrações de “curvatura de campo”, de outra natureza.)
Sobre o cálculo da excentricidade mantenedora da “asfericidade” a distâncias finitas
A relação entre a anulação da aberração “de superfície” (aberração da “esfericidade”), devida a uma determinada excentricidade da curva (elíptica) – por sua vez dependente dos índices de refração dos meios separados pela superfície – e a distância à qual se acha o objeto, cujas imagens devem se formar sobre um único ponto (“foco” imagem), independentemente da incidência sobre a superfície, pode ser buscada. De fato, pode-se cogitar, em princípio, que com uma curva de maior excentricidade seja possível obter-se a “asfericidade” para imagens de objetos situados a distâncias finitas.
Para um objeto a uma determinada distância (por exemplo, p = 120 cm), situado sobre o eixo óptico de toda e qualquer curva que separe meios com índices de refração ni = 1,0 e nr = 1,5 e tenha raio de curvatura RA = 20 cm em seu ponto apical (coincidente ao eixo óptico), isto é, com um poder focal (nr – ni)/RA = 2,5 D, e considerando-se uma incidência nula (i = 0°) formará a respectiva imagem, também sobre o eixo óptico, sempre, à mesma distância (s = 90 cm). De qualquer modo, apesar de infinitas dessas curvas serem possíveis, apenas uma elíptica terá, também, a soma a + f = 90 cm, figurando, assim, uma excentricidade específica, que será então, calculada.
Se L é a fonte de luz considerada e se Q é o ponto sobre o qual se forma a imagem da refração produzida pela incidência nula, Q será um dos focos da curva elíptica. Assim, a distância dessa fonte (L) ao “polo” (vértice) anterior da elipse (A), LA = p, é a distância do objeto à superfície; e AQ = a + f é a distância à qual se forma a respectiva imagem. (Os pontos L e Q são supostos coaxiais ao eixo maior da elipse, ou eixo óptico da superfície.) Pela lei da refração:
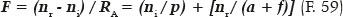
Ficam assim, automaticamente relacionadas as variáveis RA (raio de curvatura do ponto apical anterior da elipse), a (seu semieixo maior) e f (sua semidistância focal), com as que se relacionam à refração, ni (índice de refração do meio de incidência), nr (índice de refração do meio de refração), p (distância do objeto à superfície), ou F (poder focal da superfície). A distância da imagem ao polo anterior da superfície (s), como se viu, fica automaticamente determinada (s = a + f).
De fato, essa equação (F. 59) pode ser rearranjada:
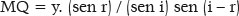
Mas como b2 = a2 – f2, vem:
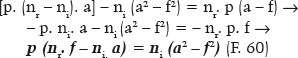
E de modo ainda mais conciso:
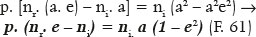
Ou, ainda, em função de RA, lembrando-se que b2 = a2 – f2 = a2(1 – e2)
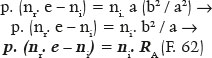
De fato, para o caso do objeto no infinito (p = ∞), resulta nr. e = ni, como já foi demonstrado. Isto é, para o objeto no infinito (p = ∞) a excentricidade da curva “asférica” (e) é igual à recíproca dos índices de refração dos meios de incidência (ni) e de refração (nr). Para a distância p = 120 cm e RA = 20 cm, ni = 1,0 e nr = 1,5, a excentricidade da curva vem a ser:
120 (1,5 e – 1,0) = 1,0. 20 → 9,0 e – 6,0 = 1,0 → e = 7 / 9 = 0,777… isto é, maior do que a excentricidade da curva esférica para o objeto no infinito (e = 1 / 1,5 = 2 / 3 = 0,666...) e que não era suficiente para anular a aberração da esfericidade para outras incidências.
O valor do semieixo maior dessa elipse (a) fica determinado por:
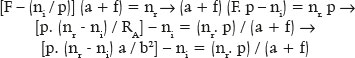
ou seja, a = 20 / [1 – (0,777...)2] = 50,625 cm; daí f = 39,375 cm e b ≈ 31,820 cm.
Entretanto, para outras incidências sobre essa superfície, a partir do ponto a 120 cm de seu ponto apical, a aberração da “esfericidade” ainda persiste, como mostra a tabela 7 (segunda coluna de valores). Enfim, para a possível anulação da aberração da esfericidade (ou da aberração de curvatura) para um ponto situado a distância finita, essa curva com excentricidade “típica” (e = 7/9) nada mostra de especial relativamente a outra (por exemplo, com e = 2/3, como visto pela Figura 16). Ela apenas representa o valor máximo da excentricidade, tal que a + f = 90 cm e RA = 20 cm. De fato, para uma elipse de excentricidade maior, como e = 0,8, com a = 50 cm e f = 40 cm, então RA = b2/a = (a2 – f2)/a = 18 cm.
Para essa família de elipses (com a + f = 90 cm e RA = 20 cm) outras excentricidades podem ser específicas para valores de outras incidências, como mostra a tabela 7. Lembre-se que para uma distância finita e uma incidência não axial, a fórmula aplicável para o cálculo em que a distância em que se forma a imagem (s) seja igual a a + f = a + ae = a (1 – e) é a F.5:
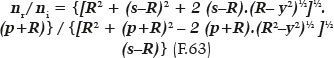
em que o valor do raio de curvatura (R) é variável conforme o ponto de incidência mas com um, específico (correspondente ao valor de y), tal que a imagem se forme à distância s = 90 cm.
Os resultados mostrados pelas tabelas 7 são paradigmáticos:
a) A segunda coluna corresponde a uma curva circular (excentricidade nula, achatamento 0). Note-se que quanto mais periférico o ponto de incidência (maior o valor do ângulo θ), mais próxima da superfície se forma a imagem correspondente (números em cor vermelha), o que significa a chamada aberração “esférica” positiva.
b) Curvas de maior excentricidade (e maior achatamento) produzirão correções progressivas dessa aberração. Por exemplo, para a de excentricidade e = 37,8858 / 52,1142 (sétima coluna a partir da esquerda) a aberração é corrigida para a incidência de 40° (a imagem forma-se exatamente a 90,000 cm, como desejado). Para essa inclinação (40°), maiores excentricidades produzirão aberrações positivas (números em cor vermelha) e as de excentricidade menores produzirão aberrações negativas (números em cor azul)com exceção para o círculo (segunda coluna), em que e = 0/20,000 = 0.
c) Não há curvas que evitem a “aberração da esfericidade” das imagens de um objeto situado a distância finita. No máximo, uma curva de certa excentricidade promove a coincidência da posição da imagem produzida pela incidência nula (no caso considerado, a 90 cm da superfície) para, apenas, outra incidência. A tabela mostra as excentricidades das curvas correspondentes às incidências de 10° a 70°, mas curvas de achatamentos intermediários entre os mostrados são também possíveis. Por exemplo, entre a de achatamento 0,3651 (que promove a coincidência para a incidência de 10°) e a de 0,3499 (que promove a coincidência para a incidência de 20°), uma curva de achatamento intermediário promoverá a imagem formada a 90 cm da superfície para uma certa incidência específica, entre 10° e 20°.
d) A curva de uma dada excentricidade produz para incidências menores do que a que promove a posição desejada da imagem (a 90 cm), aberrações negativas; e para incidências maiores do que a específica, aberrações positivas.
e) Assim, uma curva que promovesse a asfericidade total (posições das imagens sempre a 90 cm) deveria ter uma excentricidade (e, ou achatamento) decrescente, no caso, a partir da e = 7/9, terceira coluna, com o aumento do ângulo de incidência. Não seria, pois, uma curva elíptica.
f) Ainda que tal curva pudesse ser então construída, serviria para neutralizar a aberração da “esfericidade” para, apenas e especificamente, a posição do objeto a p = 120 cm (e meios de incidência e de refração como os acima considerados). Para outra distância e outros índices de refração, uma nova curva, específica para cada caso, deveria ser construída.
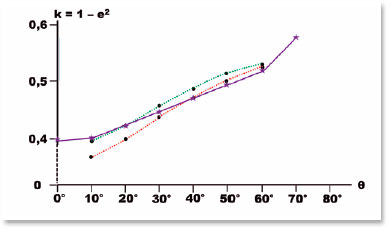
De fato, a equação fundamental pela qual se pode entender a relação entre as propriedades geométricas de uma curva elíptica e a lei básica da refração (a de Snell e Descartes) é a da F. 22, isto é, e = (sen g) / (sen j), em que j = i – w (no caso de objetos a distâncias finitas) e g = r, o ângulo de refração dado por essa incidência. Em outras palavras, a igualdade entre o ângulo de incidência (i) e o de refração (r) e que deve, sempre, obedecer a lei de Snell, subordina-se, igualmente, à geometria da elipse, com sua excentricidade (e) específica. Realmente, embora não esteja explícito na tabela 7, essa F. 22 é apenas satisfeita em uma angulação específica (i – w), correspondente a uma incidência (i) cuja relação com o ângulo de refração (r) exprima o valor da excentricidade da curva (e). As tabelas 8 e 9 mostram valores de algumas das variáveis da geometria da elipse para diferentes angulações de incidência (i) relativamente ao centro da elipse (θ), quando também variam os valores de w, para o caso das elipses com excentricidades e = (f / a) = 38,8584 / 51,1416 = 0,7598 (Tabela 8) e e = 37,8858 / 52,1142 = 0,7270 (Tabela 9). Note-se que estão destacados (em vermelho) os valores de s = 90,0000 (a posição da imagem satisfeita, em cada caso, pela refração, para os ângulos θ = 20°, na tabela 8 e θ = 40°, na tabela 9) e os das respectivas relações dos senos dos ângulos (i- w) e r, coincidentes, em cada caso, ao valor da correspondente excentricidade da curva (e = 0,7598, na tabela 8 e 0,7270, na tabela 9). Nos demais casos, essa coincidência inexiste, assim como a posição da imagem não se dá no ponto desejado (s = 90,0000 cm).
A figura 17 também mostra a relação entre o valor da variável k = 1 – e2 de uma elipse e a coordenada polar (angular) de um seu ponto (medida a partir de seu respectivo centro), cujo raio nele refratado (proveniente de incidente partindo de um objeto a distância finita) atinja o eixo óptico no mesmo local em que se forma a imagem desse objeto correspondente à incidência zero. Note-se que essa variável da elipse em que tal situação ocorre é tanto maior quanto mais periférico estiver o ponto onde a refração é considerada (linha roxa), ou seja, para cada angulação tomada a partir do centro da elipse, uma variação crescente de k (em função do valor da angulação) seria a adequada para satisfazer tal concepção. Ao contrário, para satisfazer que essa “asfericidade” desejada ocorresse para qualquer ponto da curva, a representação de um único valor de k seria a de uma linha reta horizontal (perpendicular ao eixo das ordenadas e paralela ao das abscissas).
Os diferentes posicionamentos dos centros de curvatura de cada ponto da superfície e suas consequências refratométricas
Uma das peculiaridades da curva elíptica é a de que para cada um de seus pontos haja um centro de curvatura específico. O método de sua determinação já foi, aliás, exposto (Figura 14) e o cálculo de suas coordenadas, assim como o do valor do raio de curvatura real (RP = PCP) e “aparente” (RM = PM) foram explicitados a partir da Figura 15 e pelas F.49 e F. 50 (valores das coordenadas), F. 27 e F. 43 (valores do raio de curvatura, RP, por coordenadas polares e cartesianas, respectivamente), F. 44 (valores do raio de curvatura “aparente”, PM = RM) e F. 48 (valores da relação entre RP e RM).
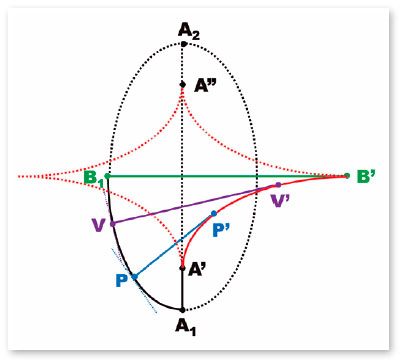
O lugar geométrico dos vários centros de curvatura, desde o do ponto apical anterior (A), RA (F. 28) ao do vértice do semieixo menor (B), RB (F. 29) e de suas relações (F. 40 a 42), passando pelos centros de curvatura intermediários é a evoluta da elipse (Figura 18).
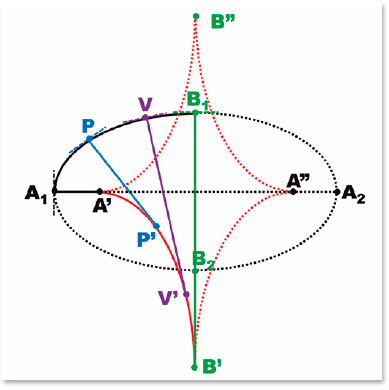
Na elipse, os pontos de maior curvatura (A1 e A2, raios de curvatura A1A’ e A2A”, Figura 18), têm os centros dos respectivos círculos osculadores (isto é, os centros de curvatura desses pontos) dentro da elipse, enquanto os pontos de menor curvatura (B1 e B2, raios de curvatura B1B’ e B2B”, Figura 18) têm os centros dos respectivos círculos osculadores (isto é, os centros de curvatura desses pontos) fora da elipse. A evoluta da elipse é descrita analiticamente pela equação:
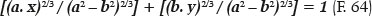
O valor do raio de curvatura (RP) de qualquer ponto de uma elipse pode ser determinado, tanto pela F. 27, quanto pela F.48. De qualquer modo, requer-se o conhecimento de duas das variáveis da elipse (a, b, f ou e, por meio das quais as outras duas são calculadas) e pela definição do ponto para o qual se requer o respectivo raio de curvatura, o que suscita a necessidade do conhecimento de duas de suas coordenadas (as cartesianas, x e y; ou uma delas e a coordenada angular θ). Assim, por exemplo, substituindo-se o valor de b2 = a2 – f2 = a2 – (ae)2 = a2 (1 – e2) na F.27, vem:
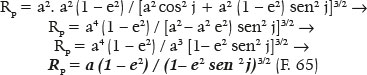
De fato, se j = 0°, RP = RA = a (1 – e2) = a. (b2/a2) = b2 / a. E se j = 90°, vem da F. 65, RP = RB = a (1 – e2) / (1 – e2)3/2 = a / (1 – e2)½ = a / (b2/a2)½ = a / (b/a) = a2/b, ratificando as F. 28 e F. 29, respectivamente.
Das F. 48 e F. 44, mas sendo, nelas, genericamente os ângulos i e r substituídos por suas versões genéricas, respectivas, j e g, em que (sen g)/(sen j) = e:
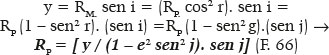
Ou, ainda, pela F. 25 (PM = RM) e F. 48:
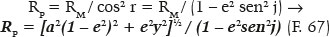
Assim, por exemplo, para a elipse com a = 50,625, e = 7/9 e θ = 10°, vem da F. 16, y = 8,594755891. Daí, pela F.25, RM = 21,08759556 e, pois, j = arc sen (y / RM) = 24,05252876°. Então, quer pela F. 65, quer pela F. 66, ou pela F. 67, vem o valor de RP = 23,44343249.
A tabela 10 mostra os valores do raio de curvatura (RP) para pontos dessa elipse, com diferentes coordenadas angulares relativamente ao centro dela (θ), assim como os de outras variáveis correspondentes. A figura 19 expõe, pictoricamente, a variação desses raios de curvatura e dos correspondentes valores dióptricos (considerou-se a curva como separando meios com índices de refração ni = 1,0 e nr = 1,5).
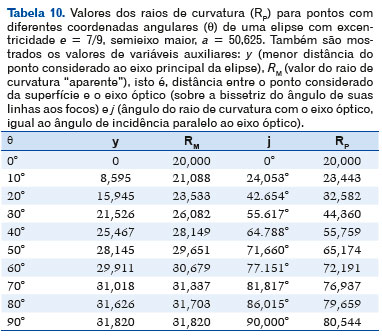
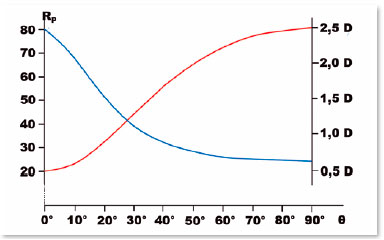
Pela figura 19 fica fácil o entendimento de que os valores dióptricos dessa curva elíptica asférica se reduzem, progressivamente, à medida que a incidência (paralela ao eixo óptico) se faça mais periférica (linha azul). Convém, todavia, observar que está sendo considerada uma curva prolata, isto é, com o eixo maior coincidente ao plano horizontal. Se a curva elíptica for girada 90° em torno de um eixo perpendicular ao plano de sua representação, passando por seu centro, seus raios de curvatura e respectivos centros não mudam relativamente à elipse, mas ela passa à forma oblata, isto é, com o eixo menor coincidindo com o horizontal (Figura 20) e, pois, com raios de curvatura decrescentes e respectivos valores dióptricos crescentes conforme incidências mais periféricas ocorrerem.
A multifocalidade das curvas elípticas
Como os valores dióptricos de uma lente em seus diferentes pontos são diretamente proporcionais aos de suas respectivas curvaturas, isto é, quanto maior a curvatura de uma superfície em um dado ponto (menor o raio de curvatura, nele), maior o seu respectivo poder dióptrico, as curvas elípticas prestam-se, naturalmente, a satisfazer o conceito óptico da multifocalidade, conforme a incidência.(e, ou a direção do raio refratado; em outras palavras, à direção do eixo visual que a atravessa).
De fato, escolhido um valor dióptrico (isto é, uma curvatura) para um determinado ponto de uma superfície, é possível fixar, para outro ponto, uma nova curvatura (maior ou menor) tal que, entre eles, ocorra uma transição (progressiva, ou regressiva) dos correspondentes valores dióptricos. Mais comum, por exemplo, é que se queira um determinado valor dióptrico para “longe” (por exemplo, + 1 D) e um maior para “perto” (por exemplo, + 4 D) que, geralmente, ocorre em posições do olhar para baixo. (Em um míope, o caso seria de uma variação de, por exemplo, – 5 D a – 2 D, também, equivalentemente maior em valores absolutos.) Mas variações regressivas (ou semiprogressivas, nomes diferentes para, basicamente, expressar o mesmo conceito) poderiam igualmente ser convenientes. Conquanto não seja objeto desta dissertação discorrer sobre as conveniências e aplicações de tais conceitos clínicos, nem sobre as dificuldades técnicas de operar suas fabricações, abordar-se-ão, apenas e brevemente, os princípios que regem essa multifocalidade, muito desejada na prática oftalmológica.
Suponha-se, então, uma curva elíptica, que represente o plano principal imagem de uma lente, isto é, o local imaginário em que se dá, nela, toda a refração dos raios incidentes (e refratados), cujo efeito seria o multifocal decrescente, em uma curva prolata (Figura 18), ou crescente, em uma oblata (Figura 20). Pela maior aplicabilidade das multifocalidades crescentes, o exemplo ficará restrito a este conceito e forma (oblata) da elipse, cuja explicitação será desenvolvida com base na figura 21.
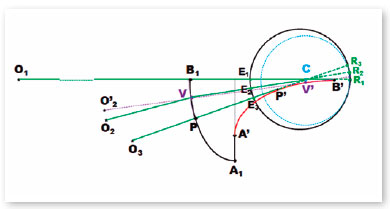
Seja R1 a imagem retínica (foveal) do objeto O1 (localizado a distância infinita) formada pela “lente” (a superfície abstrata A1B1). Assume-se que o poder dióptrico dessa superfície, no ponto B1 corrija uma eventual incorreção do sistema óptico ocular e, pois, pode ser empiricamente determinado. Note-se que o eixo visual (linha R1CE1O1) é coincidente ao raio de curvatura (B1B’) do ponto B1, isto é, tangencia a evoluta no ponto B’. Outra linha tangente à evoluta, em P’, coincide com uma nova posição do eixo visual ao fixar o objeto O3 (linha R3CE3O3) de modo que PP’ é o raio de curvatura correspondente ao ponto P, isto é, o ponto em que o eixo visual dirigido ao objeto O3 (linha R3CE3O3) cruza a superfície da elipse. O poder dióptrico de P pode ser escolhido para permitir o ajustamento óptico das imagens de objetos (O3) situados a distâncias próximas (a chamada “adição” sobre a correção óptica ajustada para a visão a “grandes distâncias”). Por isso, se os valores dióptricos estão ajustados para os pontos B1 (“grandes distâncias”) e P (“distâncias próximas”), os raios de curvatura da superfície elíptica nesses pontos serão conhecidos (em função dos valores das variáveis ni e nr) e, portanto, o perfil da curva entre os pontos B1 e P é também determinado.
Pontos intermediários da superfície, entre B1 (o de maior raio de curvatura, portanto o de menor poder dióptrico) e P (o de raio de curvatura menor, portanto o de maior poder dióptrico), apresentarão raios de curvatura intermediários e, por consequência, recíprocos poderes dióptricos cada qual com seu valor. Isso corresponde ao que se considera um efeito “multifocal” dessa interface. Note-se, todavia, que B’ e P’ são pontos da evoluta cujas tangentes coincidem com o eixo óptico do olho (o eixo visual) que passa pelos pontos B1 e P da superfície, enquanto qualquer outro ponto da evoluta pelo qual passa uma tangente (como, por exemplo, V’, que cruza a superfície no ponto V) fica abaixo do centro de rotação C (pelo qual se considera passar o eixo visual). Assim, o eixo visual através de V (R2CE2V) e o raio de curvatura da superfície nesse ponto (= VV’), embora tenham um ponto comum de coincidência (V) não são colineares. O ângulo entre essas linhas (R2VV’) é igual ao ângulo de refração (r) no ponto V, resultante de um ângulo de incidência (i) que corresponde à diferença entre as direções da posição real do objeto no espaço (O2), linha VO2 e de sua posição percebida (O’2), linha VO’2.
Embora os elementos racionais da multifocalidade em uma curva elíptica possam ser assim apresentados de modo simples, os correspondentes cálculos que lhes cabem mostram-se complexos e não serão aqui desenvolvidos.
Apêndice: esfera, esferoides e elipsoides
Refrações ocorrem em superfícies, isto é, sobre entidades do espaço tridimensional e que podem ser analiticamente descritas por valores específicos em cada um de seu eixos. Círculos, elipses e outras curvas são “figuras”, ou secções planas (no espaço bidimensional), de concretudes (do espaço tridimensional). Em outras palavras, são, apenas, representações pictóricas (linhas) de sólidos cujas superfícies (tridimensionais) separam os meios nos quais as refrações ocorrem. Assim, convém estender o estudo sobre as “realidades” das quais essas figurações agora abordadas (curvas elípticas) são, apenas, representações de simplificação. (em um plano).
Em Oftalmologia, é costumeiro que os três eixos do espaço sejam nomeados como “z” (vertical), “y” (horizontal, longitudinal, isto é, coincidente ao eixo visual) e “x”, também horizontal, mas perpendicular ao “y”, separando “esquerda” e “direita”, ou “lateral” (ou “temporal”) e “medial” (ou “nasal”), mutuamente ortogonais, isto é, cada eixo pertencente a dois planos e perpendicular ao remanescente. Assim, embora as estruturas possam ter quaisquer tamanhos, elas podem ser representadas por suas dimensões proporcionais em cada um desses eixos.
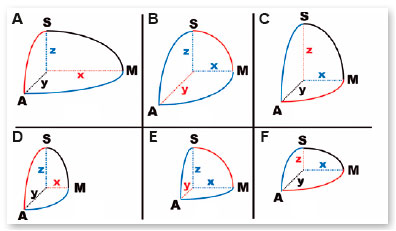
Se o volume for representado por três eixos de iguais dimensões (x = y = z), trata-se de uma esfera. Se dois deles forem iguais, mas diferentes do terceiro, as possibilidades são seis (x = y > z; x = y < z; x = z > y; x = z < y; y = z > x; y = z < x) e os volumes representados são ditos esferoides (Figura 22). Na verdade, são sólidos gerados pela revolução de uma elipse, em torno de um de seus eixos (Figura 23) e, por isso, as secções perpendiculares a esse eixo de revolução serão, sempre, representadas por círculos (daí o nome “esferoides”). Finalmente, quando os três eixos forem descritos por valores diferentes, as possibilidades são mais seis (x > y > z; x > z > y; y > x > z; y > z > x; z > x > y; z > y > x) e os sólidos chamados elipsoides escalenos. (Figura 24, mostrando um deles).
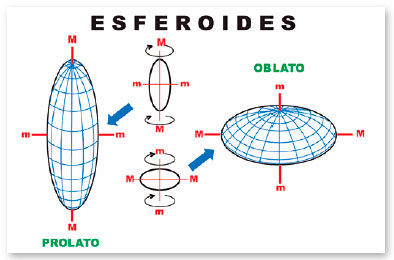
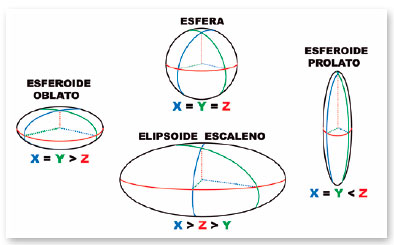
Note-se que na forma prolata (semelhante à de um quibe, uma bola de rugby, ou de futebol americano) um dos eixos é maior que os dois outros (iguais) e na oblata (semelhante à de uma drágea, ou um disco espessado em seu centro, como um “disco voador”), um dos eixos é menor que os dois outros (iguais). Entretanto, considerando-se, sempre, a posição relativa dos eixos como coincidente à do olho (y, o longitudinal, ou ântero-posterior; z, o vertical, ou súpero-inferior; e x, o transversal, ou látero-medial), as diferenças entre essas apresentações aparecem. Por exemplo, nas prolatas pela disposição do eixo maior (suas “pontas”) e nas oblatas pela disposição do eixo menor (seus “polos”).
Assim, quando o eixo maior for o y (longitudinal), a curva vertical (entre A e S) e a horizontal (entre A e M) serão elípticas e iguais entre si (Figura 22 b) e embora a aparência da superfície (como, por exemplo, a córnea) seja “cônica”, não há astigmatismo (diferença de poderes dióptricos entre elas). Assim, também, se o eixo menor for o y (longitudinal), a curva vertical (entre A e S) e a horizontal (entre A e M) serão elípticas e iguais entre si (Figura 22 e); a superfície mostra-se achatada nesses dois planos (ou meridianos) mas, também, sem astigmatismo. Quando o eixo maior ou o menor for x, o transversal (respectivamente, Figuras 22 a e 22 d), há diferença entre a curva do plano horizontal (entre A e M, elíptica) e a vertical (entre A e S, circular) e, pois, astigmatismo. No caso da Figura 22 a, o plano (ou meridiano) de curvatura menor (raio de curvatura maior, menor poder dióptrico) é o horizontal, configurando um astigmatismo “na regra”; na figura 22 d, a curvatura maior (raio de curvatura menor, maior poder dióptrico) é a horizontal, representando um astigmatismo “contra-a-regra”. Assim, também, quando o eixo maior, ou menor, for o vertical (z, respectivamente Figuras 22 c e 22 f) há diferença entre a curva no plano vertical (entre A e S, elíptica) e a horizontal (entre A e M, circular), de modo que a figura 22 c represente um astigmatismo “contra-a-regra” e a figura 22 f, um astigmatismo “na regra”. E, embora não se possa garantir (pois na composição das ametropias o fator axial seja relevante), permite-se, pelo menos, conjeturar que os erros relativos às curvaturas induzam erros refratométricos e, pois, astigmatismos, miópicos nos excessos delas (nas oblatas, Figuras 22, d, f) ou hipermetrópicos em suas insuficiências (nas prolatas, Figuras 22 a, c). Lembre-se que, nesses astigmatismos, a forma prolata, “pontuda”, o eixo maior é vertical (Figura 22 c) ou transversal (Figura 22 a); e na forma oblata, ou “achatada”, também (respectivamente, Figuras 22 d e 22 f), ao contrário da condição em que os eixos z e x aparecem iguais (respectivamente Figuras 22 b e 22 e), o que suscita interpretações aparentemente paradoxais quanto às respectivas curvaturas consideradas.
Sinopse
Introdução: Conhecimentos sobre a refração mostram-se como essenciais na prática oftalmológica. A refração é um fenômeno físico dependente da mudança da velocidade de propagação da energia radiante em sua transição de um meio de onde provem (o meio de incidência) a outro por onde segue (o de refração) e governado por uma lei de grande simplicidade, que relaciona tais velocidades (ou, equivalentemente, números relativos que as representem, os índices de refração específicos de cada um desses meios) e as direções pelas quais as frentes de onda da energia radiante se propagam. A medida dessas direções é específica a cada ponto da superfície de separação dos meios de incidência e de refração e depende de uma linha imaginária perpendicular a esse ponto (sua normal). Mas embora a refração seja um fenômeno pontual, conquanto considerada em relação às direções da energia radiante incidente e refratada, ela é, em termos mais abrangentes, dependente da superfície à qual tal ponto pertença.
Curvatura de uma superfície: A caracterização de um ponto de uma superfície é determinada por sua curvatura, um conceito que se quantifica pelo comprimento de uma linha reta, o raio de curvatura daquele ponto considerado. Na Óptica Geométrica, embora a direção em que se forma a imagem de um objeto dependa, apenas, da lei de Snell, sua posição se subordina ao raio de curvatura do ponto onde se dá a refração. O raio de curvatura é infinito nas superfícies planas, finito e constante em cada esfera (ou círculos), finito e varável em outras curvas (como as secções cônicas). Lentes corretivas de defeitos ópticos oculares são todas formadas por superfícies curvas (pelo menos uma). Textos da Refratometria Ocular abordam a refração em superfícies planas (prismas) e esférica (lentes) e a elas se limitam. A refração em superfícies esféricas é, inerentemente, defeituosa (aberrações esféricas). Lentes sem aberração esférica (chamadas “asféricas”) e multifocais exigem o desenvolvimento de ópticas baseadas na variação dos raios de curvatura em diferentes pontos da superfície refratora.
Refração em uma superfície esférica: São revistos os princípios e formulações desse tipo de refração para o caso genérico da posição da imagem de um ponto objeto situado a distância finita. E, a partir dela, suas derivadas, a equação dos raios paraxiais, a de quando se acha o objeto a distância infinita e a da formulação básica do poder dióptrico da superfície. Apesar da relativa simplicidade de seu estudo, a refração nas superfícies esféricas apresenta como consequência intrínseca a chamada aberração da esfericidade. Esta corresponde à distribuição da energia radiante incidente, por exemplo, em um feixe de raios paralelos (frentes de ondas planas) por uma extensa região do espaço onde se dão os diversos cruzamentos dos vários raios refratados, delimitada por uma superfície (a cáustica).
Superfícies asféricas: São as que concentram em único ponto (o ponto focal imagem, quando a incidência provém do infinito) toda a energia radiante refratada. A concepção exige que quanto mais distante do eixo óptico for a incidência, menor seja o raio de curvatura da superfície, comparativamente ao vértice da superfície (situado sobre o eixo óptico dela). Essa concepção corresponde ao que ocorre em elipses (e outras curvas), cujas formas podem acentuar a aberração esférica das superfícies esféricas (aberrações chamadas “positivas”), reduzi-la e até neutralizá-la (por uma superfície elíptica “asférica”) ou invertê-la (produzindo aberrações esféricas “negativas”).
A questão semântica da asfericidade: As diferentes formas com que as elipses possam ser apresentadas e seus variados resultados, suscita a discussão sobre a impropriedade do termo aberração “esférica”, por não depender exclusivamente das superfícies esféricas, podendo ocorrer (de modo “positivo” ou “negativo”) nas elipses. Propõe-se o uso dos termos de superfícies superaberrantes para quando as aberrações “esféricas” produzidas por uma esfera forem majoradas, subaberrantes quando forem reduzidas (mas não eliminadas), inaberrantes, quando forem eliminadas (as superfícies “asféricas” propriamente ditas) e contraberrantes, quando produzirem aberrações “esféricas” negativas. Por essa terminologia, qualquer superfície oblata será superaberrante, enquanto entre as prolatas poderão ser encontradas subaberrações (“positivas”), inaberrações ou contraberrações (“negativas”).
A geometria das elipses: As propriedades geométricas das elipses, seus termos e relações são suscintamente apresentados.
A refração em uma superfície sem aberração esférica: Com base nas propriedades geométricas das elipses, é examinada a condição pela qual a refração de um (qualquer) raio incidente paralelo ao eixo óptico sobre um (qualquer) de seus pontos dê um raio refratado que encontre o eixo óptico em um dos focos (o ponto focal imagem da superfície). Chega-se à formulação de que, nesses casos (incidência de frentes de onda planas), a asfericidade é conseguida quando a excentricidade da elipse (e) for igual à relação dos índices de refração dos meios de incidência (ni) e refração (nr), isto é, e = ni/nr. São desenvolvidas as equações que mostram as relações entre as diferentes propriedades da superfície e os valores de seu poder dióptrico. E os valores da excentricidade da superfície para que ela seja inaberrante (“asférica”) em função do índice de refração do meio de refração, quando o de incidência for o ar (ni = 1,0).
O posicionamento do centro de curvatura: Apresenta-se o método pelo qual se possa determinar, graficamente, a posição do centro de curvatura de qualquer ponto de uma elipse, assim como o analítico para conhecimento de suas coordenadas, do valor do respectivo raio de curvatura e demais relações entre as propriedades dessas elipses “asféricas”.
A excentricidade da curva de não aberração esférica como contingência da posição do objeto: Demonstra-se que a curva pela qual se obtém a “asfericidade” para a incidência de frentes de ondas planas (objetos situados no infinito, raios paralelos ao eixo óptico) não mantém essa qualidade para objetos a distâncias finitas, isto é, a excentricidade da curva promotora da “asfericidade” é função da distância da fonte de radiação.
Sobre o cálculo da excentricidade mantenedora da “asfericidade” a distâncias finitas: O fato de que a forma (excentricidade) da curva que proveja asfericidade para a formação da imagem (única) de um objeto situado a distância infinita não manter essa qualidade para a posição dele a outras distâncias, não significa que não se possa achar uma relação entre uma excentricidade específica e distância da fonte. Essa possibilidade é estudada, encontrando-se que há, de fato, uma excentricidade apropriada para que em uma incidência específica, a posição da imagem de um objeto situado a distância finita coincida com a que se dá pela definição do poder focal da superfície (isto é, com a da incidência nula). Contudo, para incidências menores e maiores na curva que assegure esse “pareamento” as aberrações continuam, negativas e positivas, respectivamente. Do mesmo modo, para uma certa incidência, curvas de excentricidades menores darão aberrações negativas e as de excentricidades maiores, aberrações positivas. A variabilidade da excentricidade, necessária para produzir a coincidência de imagens de um objeto situado a distância finita, em função do ângulo de incidência, significa que uma curva elíptica (excentricidade única) não pode satisfazer essa condição (“asfericidade” para objetos situados a distância finita).
Os diferentes posicionamentos dos centros de curvatura de cada ponto da superfície e suas consequências refratométricas: Retoma-se o estudo das posições dos centros de curvatura dos diferentes pontos de uma curva elíptica para descrever o “lugar geométrico” que lhes é próprio, uma nova curva, a evoluta da elipse e o que ocorre quando essa elipse é rodada em torno de um eixo perpendicular à sua figura, fazendo-a passar de uma “forma” (prolata) a outra (oblata). Embora a excentricidade (descritiva das relações “formais” da elipse) se mantenha a mesma, sua disposição no espaço (com o eixo maior na horizontal, ou na vertical) transformará variações decrescentes das curvaturas (crescentes de seus respectivos raios, nas curvas chamadas prolatas) em crescentes (nas oblatas).
A multifocalidade das curvas elípticas: A variabilidade dos valores dos raios de curvatura de uma superfície elíptica (definida por sua excentricidade) é matriz do que se chama “multifocalidade” em refratometria. Assim, lentes de poderes dióptricos crescentes (“progressivos”) ou decrescentes (“regressivos”) são simples variações de formas (excentricidades) elípticas (ainda que os cálculos – para os devidos ajustes aos valores dióptricos requeridos – possam ser complexos).
Apêndice: esferas, esferoides e elipsoides: Elipses são formas geométricas encontradas como secções de superfícies de corpos (como cones, cilindros, toros) e típicas de outros (esferoides e elipsoides). Estes são descritos em suas concepções (revolução de elipses em torno de seus eixos) e aplicações (por exemplo, na definição de astigmatismos).
REFERÊNCIAS
1. Bicas HEA, Alves AA, Uras R. Prefácio. In: Refratometria Ocular. Cultura Médica:Rio de Janeiro, C.B.O. São Paulo, 2005.
2. Bicas HEA, Alves MR. Prefácio. In: Refratometria Ocular e Visão Subnormal. Conselho Brasileiro de Oftalmologia, 4ª Ed., Cultura Médica: Rio de Janeiro, 2018.
3. Hirschberg J. The History of Ophthalmology. Vol. I: Antiquity. Transl. by F.C. Blodi. Verlag J.P. Wayenborgh: Bonn, 1982.
4. Duque-Estrada, W. Apresentação. In: Alves AA. Refração. 6ª Ed. Cultura Médica: Rio de Janeiro, 2014.
5. Duke-Elder S, Abrams D. Ophthalmic Optics and Refraction. In: Duke-Elder S. The System of Ophthalmology. Vol. V. Henry Kimpton, London, 1970.
6. Duke-Elder S. The Practice of Refraction, 8th Ed., J & A Churchill: London, 1969.
7. Prado D. Noções de Óptica, Refração Ocular e Adaptação de Óculos. Atheneu: Rio de Janeiro, 1963.
8. Uras R. Óptica e Refração Ocular. Cultura Médica: Rio de Janeiro, C.B.O. São Paulo, 2000.
9. Alves MR, Polati M, Sousa SJF. Refratometria Ocular e a Arte da Prescrição Médica. Cultura Médica: Rio de Janeiro, 2009.
10. Schor P, Uras R, Veitzman S. Óptica, Refração e Visão Subnormal. 2ª Ed. Cultura Médica: Rio de Janeiro, 2011.
11. Jesus MC. Óptica Oftálmica em Exercício. Salvador, 2005.
12. Rubin L. Optometry Handbook, 2nd Ed., Butterworths: Boston & London, 1981.
13. Helmholtz H. Monochromatic Aberrations (Astigmatism). In: Southall JPC. Helmholtz’s Treatise on Physiological Optics, Vol. I, The Optical Society of America, 1924.
14. Helmholtz H. Mechanism of Accommodation. In: Southall JPC. Helmholtz’s Treatise on Physiological Optics, Vol. I, The Optical Society of America, 1924.
15. Cowan A. Refraction of the Eye, 3rd Ed., Lea & Febiger: Philadelphia, 1948.
16. Tait EF. Textbook of Refraction. W.B. Saunders & Co.: Philadelphia & London, 1951.
17. Tschermak-Seysenegg A von. Introduction to Physiological Optics. Translated by P. Boeder. Charles C. Thomas, Springfield, 1952.
18. Gettes BC. Refraction. Little, Brown & Co.: Boston, 1965.
19. Fincham WHA. Optics. The Hatton Press, London, 1965.
20. Safir A. Refraction. Little, Brown & Co.: Boston, 1971.
21. Milder B, Rubin ML. The Fine Art of Prescribing Glasses. Trias Scientific Pub.: Gainesville, 1973.
22. Michaels DD. Visual Optics and Refraction. C.V. Mosby Co.: Saint Louis, 1975.
23. Emsley HH. Visual Optics, Vol I: Optics of Vision, 5th Ed., Butterworths: London, 1977.
24. Del Rio EG. Óptica Fisiológica Clínica. Refracción, 4ª Ed., Toray: Barcelona, 1981.
25. Miller D. Optics and Refraction. In: Podos SM, Yanoff M. Textbook of Ophthalmology, Vol. I. Gower Medical Publ.: New York & London, 1991.
26. Kuether CL. Geometric Optics, Chapter 32 (Section Refraction and Clinical Optics, A. Safir, ed.), in Thomas D. Duane Clinical Ophthalmology, vol. I, Herpes & Row, Philadelphia, revised edition, 1981.
27. Thall EH. Geometrical Optics, Chapter 30 (Section Refraction and Clinical Optics, R. J. Schechter, ed.), in Duane’s Clinical Ophthalmology, vol. I, revised edit., W. Tasman, E.A. Jaeger, eds., Lippincott Williams & Wilkins, 1998.
28. Gullstrand A. Appendices to Part I. In: Southall JPC. Helmholtz’s Treatise on Physiological Optics, Vol. I, The Optical Society of America, 1924.
INFORMAÇÃO DOS AUTORES
Financiamento: Declaram não haver
Conflitos de Interesse: Declaram não haver
Recebido em:
10 de Dezembro de 2020.
Aceito em:
23 de Outubro de 2020.